Artículo De Reflexión
Caracterización del conocimiento especializado del profesor de
matemáticas
Characterization of the specialized knowledge of the mathematics teacher
Caracterização do conhecimento especializado do professor de matemática
*Iván Andrés PAdIllA-EscorcIA
**JEnny PAtrIcIA AcEvEdo-rIncón
*Magíster en Educación, https://orcid.org/0000-0003-1210-3712,
Profesor e Investigador de la Universidad del Atlántico, Barranquilla,
Colombia.
**Doctora en Educación, https://orcid.org/0000-0003-3872-5130, Profesora de la Universidad Industrial de Santander,
Colombia.
DOI:
http://dx.doi.org/10.18634/sophiaj. 18v.2i.1175
Información
del artículo
Recibido:
marzo de 2022 Revisado: junio de 2022 Aceptado: septiembre de 2022 Publicado:
diciembre de 2022
Palabras clave: conocimiento profesional, conocimiento
especializado, profesor de matemáticas, modelo MTSK.
Keywords: professional knowledge, specialized
knowledge, mathematics teacher, MTSK model.
Palavras-chave:
conhecimento profissional, conhecimento especializado, professor de matemática,
modelo MTSK.
Cómo
citar: /how cite:
padilla escorcia, ivan, & Acevedo-Rincón , J. P.
(2022). Caracterización del conocimiento especializado del profesor de
matemáticas . Sophia, 18(2). https://doi.org/10.18634/ sophiaj.18v.2i.1175
Sophia-Educación, volumen 18 número 2.
Julio/diciembre. Versión español
Correspondencia de autor: iapadilla@mail.uniatlantico.edu.co
Resumen
En este artículo de reflexión tiene como objetivo
caracterizar el conocimiento especializado del profesor de matemáticas, desde
una mirada del modelo MTSK, cuyo rasgo principal consiste en estudiar el
conocimiento matemático y didáctico-pedagógico que requiere un profesor de
matemáticas para enseñar esta área del conocimiento en cualquier nivel
académico y que nunca antes en los modelos relacionados con el estudio del
profesor de matemáticas había sido descrito de una forma explícita, con
respecto al conocimiento que requiere un profesor para la enseñanza disciplinar
de las matemáticas, que lo hace diferenciar de otro tipo de profesionales, con
conocimiento del área. En ese orden, se presenta la estructura del modelo MTSK
expresada en dominios, subdominios, categorías de subdominios y ejemplos de las
categorías de los subdominios que contribuyen en la exploración del
conocimiento con el que debe contar el profesor de matemáticas para enseñar
contenidos de las matemáticas. Se concluye que, dada la versatilidad de este
modelo, puede ser tomado de referencia para la constitución de nuevas líneas de
investigación en el campo de la formación del profesor de matemáticas.
Abstract
In this reflection article, the objective is to
characterize the specialized knowledge of the mathematics teacher, from a
perspective of the MTSK model, whose main feature consists of studying the
mathematical and didactic-pedagogical knowledge that a mathematics teacher
requires to teach this area of knowledge in any academic level and that never
before in the models related to the study of the mathematics teacher had been
described in an explicit way, with respect to the knowledge that a teacher
requires for the disciplinary teaching of mathematics, which makes it different
from other types of professionals, with knowledge of the area. In that order,
the structure of the MTSK model expressed in domains, subdomains, subdomain
categories and examples of the subdomain categories that contribute to the
exploration of knowledge that the mathematics teacher must have to teach
mathematics content is presented. . It is concluded that, given the versatility
of this model, it can be taken as a reference for the constitution of new lines
of research in the field of mathematics teacher training.
RESUMO
Neste artigo de reflexão, o objetivo é
caracterizar o conhecimento especializado do professor de matemática, sob a ótica
do modelo MTSK, cuja principal
característica consiste em estudar
os conhecimentos matemáticos e didático-pedagógicos que um professor de
matemática requer para ensinar esta área da conhecimentos em qualquer nível
acadêmico e que nunca antes nos modelos
relacionados ao estudo do professor
de matemática foram descritos
de forma explícita, no que diz respeito aos conhecimentos que um professor
requer para o ensino disciplinar da matemática, o que o torna diferente de outros tipos
de profissionais, com conhecimento da área. Nessa ordem, é apresentada a estrutura do modelo MTSK expressa em domínios, subdomínios, categorias de
subdomínio e exemplos das categorias de subdomínio que contribuem para a
exploração do conhecimento que o professor de matemática deve ter para ensinar
o conteúdo de matemática. Conclui-se que, dada a versatilidade desse modelo,
ele pode ser tomado como referência para a constituição de novas linhas de
pesquisa no campo da formação de professores de matemática.
Introducción
A lo largo de los años, son múltiples
los cambios que han surgido en la educación; distintos modelos, teorías,
enfoques y estrategias han sido dispuestas en los procesos de
enseñanza-aprendizaje, generando impacto, repercusión y aporte en las prácticas
del profesorado. En ese orden, Schön (1983) se considera uno de los precursores
en estudiar el conocimiento profesional de un profesor que enseña un saber
disciplinar de manera general. De acuerdo
con este autor, el conocimiento de un profesor
se evidencia a partir de la reflexión
que hace desde la experiencia
de su práctica pedagógica. En el contexto de la educación matemática, Climent
(2005) afirma que el conocimiento profesional de un profesor de matemáticas es
situado y contextualizado, es decir, que el profesor desarrolla su conocimiento
de acuerdo con el entorno en donde se encuentre y no de manera individual, sino
grupal y compartido con la comunidad. No obstante, el conocimiento profesional
de un profesor es distinto al de otro, ya que este parte de las creencias y
concepciones individuales con las que este convive (Schoenfeld, 2010).
Así, caracterizar el conocimiento especializado de un profesional licenciado es uno de los desafíos más complejos
por los que ha pasado
la educación. En ese sentido,
parece necesario que un profesor
no solo debe contar
con conocimientos en el área del conocimiento del cual es profesional, sino
también contar con conocimientos pedagógico-didácticos que permitan crear
armonía en sus prácticas pedagógicas. Por ello Shulman (1986) dividió el
conocimiento del profesor en tres categorías: conocimiento del contenido de la
materia, conocimiento pedagógico del contenido y conocimiento curricular, que
se enuncian a continuación.
El conocimiento del contenido de la materia es
aquel que va más allá de los conceptos de una temática, es decir es el
conocimiento de las estructuras de la materia misma. Estas estructuras incluyen
las sustantivas y sintácticas; las estructuras sustantivas es el conocimiento del profesor para incorporar los principios y conceptos
de la disciplina que son aplicados a distintos hechos del diario vivir. Por ejemplo, el conocimiento del profesor
para aplicar el concepto de la multiplicación de números naturales que facilita la conversión de dólares a
pesos colombianos; por su parte, las estructuras sintácticas es el conocimiento
del profesor acerca de la parte formal y demostrativa de los contenidos de la disciplina, determinados por nivel
de falsedad, verdad,
validez o invalidez de los mismos. Por ejemplo, el
conocimiento del profesor para demostrar el por qué en las propiedades de la
potenciación, todo número elevado a la cero es igual 1, dado la relación de
transitividad
|
|
 |
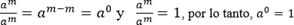Por su parte, el conocimiento pedagógico del contenido es
el conocimiento que va ligado al conocimiento del contenido desde la dimensión
de la enseñanza. Este tipo de conocimiento se compone de elementos como: las
formas de representación, analogías, ilustraciones, ejemplos, explicaciones,
estrategias y demostraciones que utiliza el profesor
para lograr que los contenidos sean más comprensibles por el estudiantado (Shulman, 1986). Por
ejemplo, en el caso de las estrategias de enseñanza, se destaca el conocimiento del profesor para saber que
representar las funciones en software especializados de la matemática como
GeoGebra, permite que los estudiantes tengan acceso al análisis de las propiedades que tienen las funciones en el plano como: dominio, rango,
período, puntos de intersección, entre otras. Esto debido a que una de
las principales funcionalidades de estos software radica
en analizar de manera profunda y robusta lo que ocurre en el plano cartesiano (Padilla-Escorcia y Acevedo-Rincón, 2021).
El conocimiento del currículo se define como el conocimiento del
profesor sobre los programas diseñados para la enseñanza de asignaturas y
contenidos concretos de una determinada área del conocimiento en cierto nivel
académico (Shulman, 1986). Además, incluye el conocimiento del propio currículo
y los diversos materiales que en este se proponen para la enseñanza, así como los tratamientos que pueden existir
para orientar una materia,
secuenciarla o las formas de evaluación propuestas en el mismo currículo
(Montes, 2015).
Así, a pesar que Shulman (1986) no abordó su modelo específicamente desde el contexto de las matemáticas, fue de gran ayuda para que los educadores matemáticos a nivel mundial decidieran
estudiar sobre el conocimiento profesional de los profesores de matemáticas. Esto, visto desde la mirada
de Montes et al. (2020),
enriquece la interpretación del investigador acerca
de la naturaleza de los profesores de matemáticas, permitiendo así evaluar las
cualidades de ellos y estudiar cómo ese conocimiento profesional se relaciona a
través del estudio de las competencias del profesor.
Algunos de los modelos más destacados se
presentan en este artículo de revisión, tales como: Bromme (1994), Fennema y
Franke (1992) y Ball et al. (2008), esto debido a que son modelos que estudian
al profesor de matemáticas y que son citados
en el modelo MTSK (Carrillo
et al., 2013; Carrillo et al., 2018), modelo en cuestión
a estudiar en este artículo.
El modelo
de Bromme
Bromme (1994) fue uno de los primeros en abordar
el conocimiento profesional del profesor de matemáticas mediante cinco dominios que conforman su modelo y que están íntimamente relacionados con lo propuesto
por Shulman (1986), estos
son: conocimiento del contenido de las matemáticas como disciplina, conocimiento de las matemáticas escolares, filosofía de la matemática escolar,
conocimiento pedagógico y conocimiento pedagógico específico de la materia, los
cuales se definen a continuación.
El
conocimiento del contenido
de las matemáticas son los aprendizajes que obtienen los profesores durante
sus estudios académicos, como,
por ejemplo, proposiciones, reglas, formas
matemáticas de pensar y métodos, que son visibles en manuales de formación de matemáticos.
El conocimiento de las matemáticas escolares es
la capacidad que tiene el profesor de comprender que los contenidos a enseñar no son simplemente las bases puras
de la materia, sino que estos más bien son adaptados
a la realidad que se vive en las escuelas.
La filosofía de la matemática escolar es el conocimiento del profesor acerca
de los fundamentos epistemológicos
de la matemática, así como del aprendizaje de las matemáticas, o las relaciones
entre las matemáticas, la vida humana y otras disciplinas.
En cuanto a lo pedagógico, Bromme (1994) estableció dos
dominios, uno general y otro específico. El general, es el conocimiento de
orientaciones sobre cómo mantener un ambiente de trabajo por grupo. Por
ejemplo, las estrategias que utiliza
un profesor para mantener la disciplina y el orden en clase (como el juego de la distensión y el juego de los aplausos).
Por otro lado, el conocimiento pedagógico específico, es aquel que está
integrado o mezclado entre el conocimiento pedagógico y la experiencia profesional
del profesor con las matemáticas, esto
debido a que no es lo mismo un profesor de
matemáticas cuya experiencia profesional es nula (recién grado de licenciado) con la de un profesor
de matemáticas con años de experiencia, ya que se espera que haya pasado
por experiencias que hayan fortalecido su práctica como profesor, que a
su vez permite una relación más profunda con sus conocimientos pedagógicos.
El modelo
de Fennema y Franke
Fennema y Franke (1992) se enfocaron en que la
enseñanza de los contenidos de las matemáticas debía darse de forma dinámica e
interactiva. Por ello consideraron, que es necesario que en el modelo del “conocimiento del profesor” los profesores cuenten
con conocimientos suficientes acerca de las matemáticas como disciplina para
poder enseñarlas. Para ello, establecieron cuatro dominios en dicho modelo:
conocimiento del contenido, conocimiento didáctico, conocimiento de la cognición de los estudiantes y las creencias de los profesores. Estos cuatro dominios se definen a continuación:
(i) El conocimiento del contenido es aquel en el cual se comprenden los conceptos, procedimientos y procesos en la resolución de problemas de situaciones del entorno que relaciona las matemáticas, así como las interrelaciones
que se dan entre los conceptos y procedimientos en este tipo de
situaciones; (ii) el conocimiento didáctico consiste en el tipo de
procedimientos, organización y técnicas motivacionales que utilizan los
profesores como estrategias en la planificación de las unidades de clase; (iii)
el conocimiento de la cognición de los estudiantes es el conocimiento de los profesores para comprender los procesos de aprendizaje de los estudiantes, esto es, lo que se le facilita y dificulta de los
diferentes contenidos de las matemáticas; (iv) las creencias de los profesores
son las percepciones que influyen
en la comprensión de estos en la enseñanza de las matemáticas, dependiendo del contexto en el que se encuentre y de las
experiencias con las que cuente.
El modelo
de Ball y sus colaboradores
En esa misma década Deborah Ball y sus colaboradores, en el grupo de investigación de matemática educativa de la Universidad de Michigan en el año 2008, afinaron el modelo propuesto por Shulman en los 80. Su preocupación estaba puesta en estudiar el conocimiento del profesor de
matemáticas, con la idea de darle más finura a esa profesión, de manera que se
pudieran establecer diferencias marcadas entre los profesores de matemáticas
con los demás profesionales que también tienen conocimientos del área. Para
esto, los dominios que proponía Shulman (el conocimiento de los contenidos y el
conocimiento didáctico de los contenidos) fueron la base en este modelo
denominado “Conocimiento Matemático para la Enseñanza” (Ball et al., 2008),
cada uno con tres respectivos subdominios.
En lo referente al conocimiento del contenido, Ball et al.
(2008) propusieron los siguientes tres subdominios: conocimiento común del
contenido, conocimiento especializado del contenido y conocimiento del
horizonte del contenido, los cuales se definen a continuación: (i) El
conocimiento común del contenido es el conocimiento utilizado en situaciones
que no son exclusivas de la enseñanza, es decir que cualquier persona formada
en matemática podría poseer. Por ejemplo, la noción de saber cuándo una
fracción con igual denominador es mayor o menor que otra a través de análisis
de cantidad y repartición; (ii) El conocimiento especializado, que es el conocimiento de las habilidades netamente matemáticas que requiere un profesor para la enseñanza y que se considera
el aporte más significativo que se resalta
en este modelo, puesto que condujo a pensar
en la necesidad de que la enseñanza
de las matemáticas estuviera a cargo de profesionales con formación
en Educación Matemática y que algunas de las tareas más recurrentes que debería
cumplir un profesor con conocimiento especializado en las matemáticas fueran:
presentar ideas matemáticas, encontrar ejemplos para abordar un tema matemático específico, relacionar un tópico con otro de años anteriores o posteriores, modificar tareas para hacerlas más
complejas o sencillas, evaluar los argumentos de los estudiantes, usar el
lenguaje formal de las matemáticas en las definiciones, entre otras (Montes,
2015); (iii) El conocimiento del horizonte matemático es el nivel de conciencia
de los profesores acerca de cómo están distribuidos los contenidos de
matemáticas en el currículo, de manera que esté en la capacidad de establecer
relaciones entre los contenidos dependiendo
de los distintos niveles de escolaridad; estas
pueden ser, además,
dentro del mismo
concepto (intra conceptuales) o entre diferentes conceptos (inter conceptuales). Por ejemplo, un profesor de primaria debe saber
los conocimientos e interpretaciones que requieren sus estudiantes acerca de
los números fraccionarios para luego afrontar los números racionales en los
grados de secundaria (conexión interconceptual).
En cuanto al conocimiento didáctico
del contenido, Ball et al. (2008) propusieron los siguientes tres subdominios:
conocimiento del contenido y los estudiantes, conocimiento de la enseñanza del
contenido y conocimiento curricular, los cuales se enuncian a continuación: (i)
El conocimiento del contenido y los estudiantes es el conocimiento que mezcla conocer
a los estudiantes y a los contenidos de matemáticas a partir de las dificultades,
obstáculos y necesidades más frecuente que
enfrentan los educandos en el aprendizaje de los tópicos. Por ejemplo, el
conocimiento que tiene el profesor para identificar que las principales causas
que llevan a malos rendimientos de los estudiantes en el aprendizaje del
Álgebra se derivan de dificultades de operar números naturales, enteros y
racionales; (ii) El conocimiento de la enseñanza del contenido es definido como
la mezcla de conocer la enseñanza y los contenidos de matemáticas, esto para diseñar
estrategias, unidades didácticas y actividades que permitan
facilitar el aprendizaje de los educandos con base en los errores con los que
estos cuentan. Por ejemplo,
en la enseñanza de fracciones utilizar elementos de la vida real como galletas, manzanas, chocolate, entre otros y
repartirlos en partes iguales son situaciones que permiten comprender la
esencia del concepto de fracción;
(iii) El conocimiento curricular es el conocimiento acerca de los objetivos y fines curriculares que guían la práctica
pedagógica del profesor de matemáticas, siendo muy similar a lo anterior a lo
propuesto en los 80 por Shulman (1986).
No obstante, cabe destacar que una de las principales
dificultades que se encontraron en este modelo estuvo en determinar lo que es
considerado como conocimiento común y conocimiento especializado en
matemáticas, ya que de acuerdo al nivel de escolaridad en el que se encuentre
enseñando matemáticas un profesor, se podría
afirmar si tiene o no conocimiento especializado de un contenido en específico
(Flores, Sosa y Ribeiro, 2016). Por ejemplo, una persona del común por
intuición podría saber que el número decimal 2.405 es menor que el número
decimal 2.41, sin embargo, un profesor con conocimiento especializado del tema
sabe, que 2.405 es menor a 2.41, porque en la comparación de las centésimas del
número decimal 0 es un número menor a 1.
El modelo propuesto por Ball et al., (2008) a
pesar que ofreció mayor claridad y explicites en cuanto a detallar el conocimiento que requiere el profesor
para la enseñanza de las matemáticas, abordando aspectos como el conocimiento de la enseñanza
y el conocimiento del profesor
sobre el aprendizaje de sus estudiantes, en cuanto al dominio
didáctico-pedagógico. Se considera que dejó abierta a la interpretación del
lector y de la literatura el subdominio de conocimiento especializado del
profesor, el cual propusieron como una manera de diferenciarlo del conocimiento
común de un profesional con conocimiento matemático, claro está que Ball y
colaboradores pensaron en este subdominio como algo más de tipo matemático, por
lo que habría sido interesante mirarlo desde el saber didáctico-pedagógico, que
se espera logren los licenciados en matemáticos, y no profesionales como matemáticos, físicos, ingenieros, entre
otros, en cuya formación no se contempla
lo antes en mención. De igual
manera, en este subdominio más allá de que haya sido pensado
netamente en el plano disciplinar, tampoco evidenció de manera
explícita, en qué conocimientos de las matemáticas se diferencia alguien
con conocimiento
especializado de alguien con conocimiento común.
Conocimiento especializado del profesor de matemáticas (MTSK)
El modelo denominado Mathematics Teacher Specialized
Knowledge (MTSK), en Español “Conocimiento especializado del profesor de
matemáticas” es generado en el seno del grupo “Seminario de Investigación en
Educación Matemática” (SIDM) y coordinado desde la Universidad de Huelva en España. De acuerdo con Carrillo
et al. (2018). Este modelo, surge desde una necesidad de complementar trabajos
realizados por Fennema y Franke (1992), Bromme (1994), Ball et al., (2008), entre otros, con respecto a la profesionalización del profesor de matemática, así como una oportunidad de ser tendencia dentro de nuevas
líneas de investigación que estuvieran
encaminadas al análisis del profesor
de matemáticas, como oportunidad de mejora para su práctica
pedagógica. Es por eso, que este modelo se centra en el conocimiento profesional que necesita
y usa el profesor para explicar y comprender la naturaleza de las matemáticas. Por tal motivo
no abarca los conocimientos generales pedagógicos de los profesores (Pedagogía y Psicología) al no
ser estos específicos de las matemáticas.
Este modelo consta de dos dominios. Por una parte,
el conocimiento de las matemáticas (MK), el cual representa una red de conocimientos estructurada de acuerdo con reglas y
conexiones que permiten comprender la naturaleza de las matemáticas, la razón y
el origen de los procedimientos, el lenguaje matemático y su precisión; además,
abarca el conocimiento matemático que el profesor usa, o puede usar, en
cualquier actividad y que trasciende aún más del contenido matemático que se pretende
que aprenda un estudiante del nivel académico en el que enseña, no
solamente en cantidad de conocimiento sino también en la naturaleza de este, es
decir en las diversas aplicaciones que tienen los contenidos de las matemáticas (Carrillo et al., 2018; Advíncula et al., 2021). De este se desprenden los
siguientes tres subdominios: conocimiento de los temas (KoT), conocimiento de
las estructuras matemáticas (KSM) y conocimiento de las prácticas matemáticas
(KPM).
1.
Por otro lado,
el dominio conocimiento pedagógico del contenido (PCK)
que se basa en las formas de profundizar
el contenido matemático cuando se tiene la intención de enseñanza y aprendizaje
(Rojas, Flores-Medrano y Carrillo, 2015; Vasco y Climent, 2018). A su vez, se desprenden los siguientes tres subdominios: conocimiento de
las características de aprendizaje en matemáticas (KFLM),
conocimiento de la enseñanza de las matemáticas (KMT) y conocimiento de los
estándares de aprendizaje matemáticos (KMLS).
A su vez, cada uno de los seis subdominios antes mencionados, giran alrededor de las creencias
y concepciones con las que cuentan los profesores
con base en las experiencias que tienen en la enseñanza de las matemáticas, y que son identificadas como la filosofía de las matemáticas, como componente dentro del conjunto de conocimiento
del profesor (Carrillo
et al., 2017). Así, en la Figura 1 se muestra la forma en cómo están distribuidos los dominios
y subdominios de conocimiento del modelo. En la parte de la izquierda del
modelo se ubica el conocimiento matemático (MK) y sus 3 subdominios:
conocimiento de los temas (KoT), conocimiento de las estructuras matemáticas (KSM) y conocimiento de las prácticas
matemáticas (KPM); por su parte, en la derecha del modelo,
se ubica el dominio de conocimiento didáctico-pedagógico (PCK) y sus 3
subdominios: conocimiento de la enseñanza de las matemáticas (KMT),
conocimiento de las características de aprendizaje de las matemáticas (KFLM) y conocimiento de los estándares de aprendizaje de las matemáticas (KMLS); en el centro del modelo se ubican las creencias y percepciones del profesor de y como estas subyacen
en cada subdominio de conocimiento, como se observa en la Figura
1:
Figura 1. Modelo del conocimiento especializado del profesor de
Matemáticas
Fuente: Carrillo et al. (2018).
Ahora bien, el KoT, en Español
conocimiento de los temas, no se refiere solamente al conocimiento de la matemática como disciplina, sino que incluye a la matemática escolar. Es decir,
describe qué y cómo conoce
el profesor de matemáticas
los temas que va a enseñar, el conocimiento fundamentado de los contenidos
matemáticos (conceptos, procedimientos, hechos,
reglas, teoremas, lemas,
etc.) y sus significados, además
de las conexiones que se establecen entre los diferentes contenidos y
las maneras de utilizar los registros de representación (Escudero y Carrillo, 2020).
En el KoT se visionan
cinco categorías de acuerdo con lo aportado
por Flores-Medrano et al.
(2014) en su tesis de doctorado y que son indispensables para todo profesor que
enseña matemática.
1.
La fenomenología de los contenidos corresponde al conocimiento del profesor sobre
el uso y aplicaciones de un tema en específico dentro de las propias matemáticas (intra conceptuales), así como sobre situaciones de la vida real dentro de las cuales el profesor puede ubicar un tema (Vasco, Climent, Escudero, Montes & Ribeiro,
2016). Por ejemplo, el conocimiento del profesor para identificar que la
representación de la transmisión de una enfermedad o el drenado de un tanque
pueden estudiarse utilizando una ecuación diferencial.
2.
La categoría propiedades y fundamentos atribuibles a un tema
en particular corresponde al conocimiento del profesor acerca del uso de propiedades y reglas de los contenidos particulares en las matemáticas.
Por ejemplo, el conocimiento del profesor acerca de las propiedades de la
potenciación que debe tener en
cuenta
para solucionar una expresión algebraica con potencias. Esto se observa en la
siguiente operación combinada con potencias
; en esta, utilizar las propiedades de las potencias de manera independiente contribuye a solucionar el ejercicio de manera más rápida y sencilla, inicialmente aplicando la propiedad producto
de potencias de bases iguales
el resultado sería
, luego
la propiedad cociente
de potencias
de bases iguales que da como resultado
X4 . Así mismo, la diferencia entre propiedades dependiendo de la estructura matemática en la cual se esté abordando un
contenido; por ejemplo, las matrices no cumplen con algunas propiedades de
estructura algebraica, como la propiedad conmutativa, que sí cumplen las
operaciones básicas de adición y multiplicación en los números reales.
3.
Los registros de representación son los conocimientos
del profesor acerca de las distintas formas en que puede representarse un contenido, bien sea gráficamente, verbalmente, numéricamente, analíticamente, etc. Por ejemplo, los conjuntos que pueden representarse por
comprensión o por extensión. Así: A= {el conjunto de los números impares
menores a 21} o A= {1, 3, 5, 7, 9, 11, 13, 15, 17,19}; así mismo ocurre en las
fracciones, las cuales pueden ser representadas de manera gráfica, concreta,
verbal o simbólica.
4.
Las definiciones son el conocimiento del profesor para, de
acuerdo con las propiedades que se cumplen en las matemáticas, definir un tema
en específico. Por ejemplo, la definición de un número impar teniendo en cuenta que este debe ser de la forma
2+1 o 2+3, la definición de un triángulo rectángulo, a partir
de que a lo sumo debe tener
un ángulo recto (90°).
5.
La categoría de procedimientos es
el conocimiento del profesor sobre
los algoritmos convencionales y alternativos que se utilizan en los contenidos de la matemática; es el conocimiento que tiene el profesor para responder preguntas
que formulan los estudiantes como: ¿Cómo se hace? ¿Por qué
se hace así? ¿Por qué se utiliza
así? o ¿Qué quiere decir
eso? Un ejemplo de esto es, el conocimiento
del profesor para saber por qué el rango de la función
trigonométrica establecida por la fórmula
es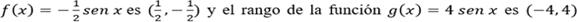 
entre otros
ejemplos propuestos por Aguilar-González, Muñoz-Catalán y Carrillo
(2019) sobre el conocimiento del profesor de las propiedades y elementos (ángulos,
lados y vértices) que se utilizan para definir a los polígonos en Geometría.
El KSM, conocimiento de las
estructuras matemáticas, en
Español, corresponde al constructo personal que el profesor desarrolla sobre la
forma en que están conectados internamente las temáticas de matemáticas para
relacionarlas entre sí, bien sea del curso que está impartiendo o con
contenidos de otros cursos o niveles superiores (Montes, 2015; Vasco y Climent,
2018), de manera que en dichas relaciones permiten incrementar o simplificar el grado de complejidad de
una temática en específico (conexiones inter conceptuales e intra
conceptuales), es decir
dentro del mismo campo de las matemáticas. (Flores-Medrano et al., 2016). Ahora bien,
las conexiones inter conceptuales son ideas matemáticas que vinculan
representaciones del mismo concepto o diferentes; las conexiones intra
conceptuales son ideas
matemáticas que tienen
lugar en la proximidad de un único concepto (Martínez et al.,
2011). Así mismo, Flores-Medrano et al. (2014) propone cuatro categorías acerca del conocimiento del profesor de matemáticas para establecer conexiones en los contenidos que enseña; estas son:
las conexiones de complejización, simplificación, transversales y auxiliares.
1. Las conexiones
de complejización, son los conocimientos del profesor para relacionar los
contenidos enseñados con contenidos posteriores, es decir
una visión de la matemática elemental desde un punto de vista
avanzado de lo particular a lo general.
Por ejemplo: el conocimiento del profesor para relacionar que la enseñanza de la factorización será
fundamental en el aprendizaje del límite de funciones; así mismo, el
conocimiento del profesor para relacionar las nociones geométricas que
desarrollan los estudiantes (recta, punto, ángulo, polígonos) en primaria, con
la demostración de teoremas de geometría euclidiana en secundaria.
2.
Las conexiones de
simplificación son los conocimientos del profesor para relacionar los
contenidos que enseña con contenidos anteriores, es decir previamente abordados
por sus estudiantes. Por ejemplo, en la realización de la derivada de la
función expresada por la fórmula , se denota el conocimiento del profesor para factorizar,
tanto el numerador como el denominador; en el caso del numerador:
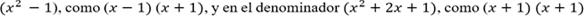
, lo que se considera
como conexión interconceptual. En este caso la función se reduce a , la cual es mucho más sencillo
de derivar que como estaba propuesta originalmente.
3.
Las conexiones de contenidos transversales son los
conocimientos del profesor para relacionar contenidos comunes de diferentes
tipos de pensamientos matemáticos, como, por ejemplo, el límite, la derivada, y
la continuidad puntual y global que subyacen a procesos infinitos, o también la
relación que menciona Climent et al. (2021) de que la igualdad
está presente en expresiones numéricas
y algebraicas (pensamiento
numérico) y que se relaciona a su vez con la congruencia de figuras geométricas
y la semejanza (pensamiento geométrico).
4. Por último, las conexiones
auxiliares son los conocimientos del profesor para realizar conexiones de
tipo inter conceptual que no hacen
parte del contenido que se está enseñando y que contribuye en la solución del problema que se esté
desarrollando. Por ejemplo, en el límite 
,
al ser esta una operación cuyo resultado es igual a una indeterminación de la
forma: 
si
se reemplaza el valor de x , se hace uso de la regla de L’Hopital como conexión auxiliar, ya que, mediante
el concepto de derivada se deriva tanto el numerador y denominador de la
función, hasta que se desaparezca la indeterminación en esta.
Por su parte,
el KPM, conocimiento de las prácticas matemáticas en español, es el conocimiento específico del profesor para
demostrar, justificar, validar, hacer deducciones e inducciones y generar
conocimiento en matemáticas, es decir su significado puro. Así mismo, es el conocimiento del profesor sobre la organización jerárquica, las formas de
proceder en la resolución de problemas matemáticos, el buen uso de símbolos
formales en matemáticas y las condiciones
necesarias y suficientes que se requieren para generar una definición en
matemáticas. Además, el conocimiento del profesor acerca de prácticas particulares de las matemáticas como la modelación (Montes, 2015; Aguilar-González, Muñoz-Catalán y Carrillo, 2019;
Flores-Medrano et al., 2016; Padilla-Escorcia y Acevedo-Rincón,
2020 y Zakaryan y Sosa, 2021).
Ahora bien, Flores-Medrano et al. (2014) proponen categorías que están ligadas
al conocimiento de las prácticas de los profesores de matemáticas. Estas
son: prácticas ligadas
a las matemáticas en general
y prácticas ligadas a una temática en matemáticas, que
se definen a continuación:
1. prácticas
ligadas a la matemática en general son el conocimiento del profesor para
saber cómo se desarrollan las matemáticas independientemente del concepto
trabajado y de las estructuras lógicas de pensamiento que contribuyen a
comprender el funcionamiento de múltiples aspectos matemáticos; por ejemplo, el
conocimiento del profesor acerca de que los puntos de acumulación, puntos de
adherencia, o puntos interiores son
conceptos que a partir de su abstracción se derivan de conceptos de la
topología general.
2. prácticas ligadas a una temática en matemáticas son el conocimiento del profesor acerca de los contenidos a impartir
desde su estructura matemática; por ejemplo,
saber el significado de una condición necesaria y una condición suficiente para trabajar
genéricamente en matemáticas, lo cual permite la creación de estructuras
lógicas de pensamiento que pueden mejorar el entendimiento de fenómenos
cotidianos (Montes, 2015).
El
KFML, conocimiento de las características de aprendizaje, en Español, está enfocado en reconocer a los contenidos de las matemáticas como objetos de aprendizaje (Escudero
y Carrillo, 2020; Aguilar-González et al., 2018), esto
es,
el conocimiento del profesor para comprender las relaciones que establecen los estudiantes con los conceptos
trabajados, así mismo,
las capacidades y debilidades que tienen acerca de estos. Es decir,
que el profesor sepa cómo
aprende el estudiante y cómo desarrollan la cognición los estudiantes de
acuerdo con las temáticas abordadas. De igual manera, el conocimiento de los
obstáculos, dificultades y errores que más presentan los estudiantes al
aprender los contenidos de las matemáticas.
Ahora bien, Escudero-Ávila y Carrillo (2020)
proponen que este subdominio del MTSK, se desprende en las siguientes categorías: fortalezas y dificultades asociados al aprendizaje de un contenido matemático, formas de interacción de los estudiantes con un contenido
matemático, intereses y expectativas de los estudiantes y teorías de
aprendizaje asociadas a un contenido matemático.
1. el conocimiento de las fortalezas y dificultades asociadas al aprendizaje de los contenidos matemáticos es el conocimiento del profesor acerca
de las concepciones erróneas que existen sobre
un determinado tema por
parte de un estudiante y que son propias del contenido matemático
específico, es decir, que están
asociadas directamente con las características matemáticas y no pedagógicas del contenido. Sumado a esto, en esta categoría también
se encuentra el conocimiento de las ideas matemáticas incorrectas que los
estudiantes pueden adquirir de un contenido de las matemáticas. Un ejemplo de
esto son las dificultades que presentan los estudiantes para interpretar gráficamente el concepto de rango de la función
trigonométrica seno, debido a que no comprenden el concepto de rango de
una función en general.
2.
El conocimiento de las formas
de interacción de los estudiantes con un contenido matemático se refiere al conocimiento que tiene el profesor
sobre los procesos
y estrategias de los estudiantes, tanto los típicos como los no habituales en el aprendizaje de las matemáticas; incluye también el conocimiento del profesor
sobre los posibles modos de los estudiantes de construcción de
conocimiento asociados a la naturaleza misma del contenido matemático. Un
ejemplo de esto es el conocimiento del profesor acerca de que la estrategia que utilizan los estudiantes para sumar o restar números
racionales heterogéneas es el método de la “carita feliz” o cruzado por
encima del método del mínimo común múltiplo, incluso cuando se trata de más de
tres números racionales los que se operan.
3.
En cuanto al conocimiento de los intereses y expectativas de los estudiantes sobre el contenido matemático, son los conocimientos del profesor acerca
de las expectativas e intereses
de los estudiantes con respecto al aprendizaje de las matemáticas, además
del conocimiento sobre
las preconcepciones de facilidad
o dificultad asociadas comúnmente a las distintas áreas de las matemáticas con
las que cuentan los estudiantes
4.
Teorías de aprendizaje asociadas a un contenido matemático es el
conocimiento que tiene el profesor de
las posibles formas de aprehensión asociadas a la naturaleza del contenido
matemático. Incluye el conocimiento de teorías
sobre el desarrollo cognitivo del estudiante, tanto para la matemática en general
como para contenidos particulares, las cuales provienen
de la experiencia profesional del profesor o de la investigación sustentada en teorías que permitan explicar los
procesos de construcción de conocimiento matemático desde la
mirada de la enseñanza y aprendizaje (Escudero-Ávila, 2015).
Por otro lado, en cuanto al KMT, conocimiento
de la enseñanza de las matemáticas, en Español, es el conocimiento del profesor
acerca de teorías formales de la enseñanza de las matemáticas, derivadas de
investigaciones en Educación Matemática o de observaciones y reflexiones de las actividades de matemáticas en el salón
de clases. Este se enfoca en las habilidades y el grado de conciencia que posee el profesor en la selección y uso de estrategias
a nivel conceptual o pedagógico para la enseñanza de las matemáticas
(Delgado y Zakaryan, 2019; Montes, 2015). En ese orden, Flores et al. (2014)
propuso tres categorías que caracterizan el conocimiento del profesor desde la
mirada de la enseñanza de las matemáticas, estas son: teorías personales e
institucionalizadas de enseñanza, conocimiento acerca
de recursos materiales y virtuales y el conocimiento de las estrategias, técnicas, ejemplos y tareas para la enseñanza del contenido
matemático, las cuales se definen a continuación:
1. Teorías personales e institucionalizadas de enseñanza son los conocimientos del profesor sobre las teorías de enseñanza en Educación Matemática, como, por ejemplo, la
teoría de las situaciones didácticas que propone Brousseau y las situaciones
que pueden darse en la misma [acción, formulación, validación e institucionalización] y que sirven para planificar actividades o estrategias en clase. Además, el conocimiento
para identificar el nivel de potencialidad que ofrecen este tipo de actividades, talleres y unidades didácticas
propuestas, o el conocimiento de ejercicios, metáforas, explicaciones y analogías
que conoce el profesor e influyen en el aprendizaje e interpretación de los estudiantes en los contenidos. Por ejemplo, la enseñanza
de los números primos utilizando la criba de Eratóstenes en material concreto
(cartulina).
2.
El conocimiento acerca de recursos
materiales y virtuales
es el conocimiento para enseñar matemáticas mediante libros de textos,
regletas, pizarra normal y electrónica, tangram, softwares especializados del
área, entre otros.
3.
El conocimiento de las estrategias, técnicas, ejemplos y tareas para la enseñanza del contenido matemático es el conocimiento que tiene el profesor acerca
del potencial que ofrecen las actividades, tareas,
ejemplos, estrategias (incluye el uso de analogías para la enseñanza) o técnicas didácticas en la enseñanza
de los contenidos de las matemáticas (Espinosa-Vásquez, Zakaryan y
Carrillo, 2018). Un ejemplo de esto sería cuando un profesor enseña las tablas
de distribución de frecuencia en estadística y propone una tarea en la cual
sean los mismos estudiantes quienes recojan la información a tabular por medio
de una encuesta y un tema que sea de su interés.
Por su parte, en la categoría de ejemplos, esta puede hacerse visible cuando un profesor
propone diferentes ejercicios para explicar el rango de la función
trigonométrica seno,por ejemplo,
o cuyo comportamiento depende de la constante que acompaña al argumento de la función
con forma , en este caso a.
El KMLS, conocimiento de los estándares de aprendizaje de las matemáticas, en Español,
corresponde al conocimiento del profesor acerca de los
resultados de aprendizaje que espera tengan sus estudiantes dependiendo del
nivel escolar en el que se encuentren, además del nivel de profundización con el que debe ser enfocado un contenido
de matemáticas a partir de los niveles
escolares y los estándares e indicadores nacionales e internacionales de
aprendizaje, los cuales indican la organización de las temáticas con base en
cursos previos (Muñoz-Catalán, Liñan y Ribeiro, 2017). En ese sentido,
Flores-Medrano et al. (2014) presentaron una serie de categorías que
profundizan el conocimiento especializado del profesor en este subdominio. Estas son: Conocimiento que tiene el profesor acerca de los contenidos matemáticos que
se requieren en el grado escolar en el que se está impartiendo clases,
conocimiento del nivel
de desarrollo conceptual y procedimental esperado
para un tópico
en un determinado momento
escolar y conocimiento de la secuenciación de diversos temas
ya sea dentro del mismo curso o pensando en cursos
anteriores o posteriores, las cuales se definen a continuación:
1.
Conocimiento que tiene el profesor acerca de los contenidos
matemáticos que se requieren en el grado escolar en el que se está impartiendo clases, este conocimiento puede ser adquirido por el profesor por medio de un documento que
indique cuáles son esos contenidos o cuál es el nivel de abstracción que deben
desarrollar los estudiantes en dichos grados. Por ejemplo, en los Derechos
Básicos de Aprendizaje Volumen 2, propuestos por el Ministerio de Educación Nacional
(MEN, 2016) se evidencia que los estudiantes en los grados de
primero a tercer grado deben tener la capacidad de resolver ejercicios de las
operaciones básicas en matemáticas, lo cual debe ser de conocimiento del
profesor que enseña matemáticas en educación básica primaria.
2.
Conocimiento del nivel de desarrollo conceptual y procedimental esperado para un tópico en un determinado momento escolar se refiere al
conocimiento acerca de la profundidad con la que debe abordarse un contenido de
acuerdo con un determinado ciclo escolar. Por ejemplo, saber qué tipo de
clasificaciones entre polígonos se esperaría que un estudiante hiciera al
finalizar la primaria (quinto grado).
3.
Conocimiento de la secuenciación de diversos temas ya sea dentro
del mismo curso o pensando en cursos anteriores o posteriores es el
conocimiento del profesor acerca de las ideas o nociones previas que tiene un
estudiante acerca de un contenido en término de lo que enmarca el contenido
curricular, antes de conocer una temática a desarrollar. Por ejemplo, el
conocimiento del profesor de las ideas de multiplicación que tienen sus
estudiantes cuando profundizan esta operación matemática en el tercer grado.
Aplicación del MTSK en la Educación Matemática
El modelo MTSK ha tenido impacto significativo en la comunidad
académica, especialmente en territorio español, país en el que surge en el año 2013 y en el que toma auge. No obstante, con el pasar
del tiempo diversos
autores han profundizado en este modelo, anexando nuevas categorías y
características a cada uno de los subdominios de los dominios que conforman el
mismo. En ese orden, desde el año en que se constituyó el modelo, se han
realizado diversos artículos, capítulos de libro publicados por los miembros
del grupo SIDM, tesis doctorales dirigidas por los miembros del grupo antes
en mención y cinco Congresos Iberoamericanos sobre el conocimiento
especializado del profesor de matemáticas; congreso en el cual se discuten
experiencias alrededor del uso del MTSK como herramienta para el análisis
del quehacer docente,
siendo el último congreso del MTSK, realizado
en el mes de noviembre de 2021 en Brasil. De esta manera,
estas acciones académicas han contribuido a formar la Red
Iberoamericana MTSK, conformada por miembros de los siguientes países: España, Portugal,
México, Costa Rica, Venezuela, Colombia, Ecuador, Perú, Chile, Brasil,
Argentina y otros países europeos,
como Italia y Alemania
(Carrillo, 2019).
En ese orden ideas, son los profesores en formación
inicial, profesores en ejercicio y profesores en formación continuada (profesores en ejercicio cursando
estudios de perfeccionamiento), los participantes que en su mayoría
han servido de muestra para las investigaciones referentes a la caracterización de su conocimiento especializado. En el caso de los profesores en formación inicial,
se ha explorado acerca del conocimiento especializado de los profesores que se están formando para ser profesores de
Educación Básica Primaria; no obstante, en este modelo es aún una deuda la
exploración del conocimiento especializado de profesores de matemáticas que se
están formando para la Educación Básica Secundaria o Media acerca de la
enseñanza de cualquier contenido de las matemáticas relacionados con estos
niveles de escolaridad, muy a pesar que Muñoz y Montes (2016) aseguran que en el contexto de la educación secundaria es relevante este modelo debido
al énfasis que se hace
al conocimiento didáctico-pedagógico de los
contenidos, el cual en la realización de procesos de investigación ha sido
escasamente explorado, a pesar de que es muy común encontrar en los salones de
clases evidencias de subdominios del MTSK como es el caso del KMT y KFLM en los
procesos de enseñanza. En cuanto a los profesores en ejercicio, ocurre un caso
contrario a los profesores en formación inicial. Esto es, al ser profesores que
ejercen su rol y su práctica día a día, han sido más explorados con respecto a
su conocimiento sobre la enseñanza de diversos contenidos de las matemáticas.
Muñoz y Montes
(2016) también resaltan
la importancia de estudiar el modelo MTSK en el contexto de profesores
de educación infantil, puesto que le permite otorgar mayor profundidad y rigor
matemático al conocimiento que exponen los profesores, ya que, a pesar del
carácter elemental de los conceptos en este nivel académico, es necesario que quien enseña
tenga claridad de dónde, para qué y por qué surge lo que enseña.
Es por eso que uno de los desafíos a futuro de este
modelo, es expandirse al profesorado de Educación infantil en Matemáticas, ya
que en muchas ocasiones los profesores que enseñan en estos niveles
de escolaridad no cuentan con formación
en matemáticas.
No obstante, son múltiples los diferentes contenidos que han sido estudiados de acuerdo con el modelo MTSK. En las más recientes Actas del Seminario de Didáctica de las Ciencias
y las Matemáticas en la Universidad de Huelva
del
año 2017 y 2019 se evidenció que han sido explorados el conocimiento especializado del profesor que enseña
matemáticas en temáticas tales como: resolución de problemas de magnitudes proporcionales (Barrera, Liñán y Pérez,2017); conocimiento emocional y especializado del profesor de matemáticas; conocimiento especializado para la enseñanza de la geometría en Educación
Infantil (Escudero-Domínguez, Muñoz-Catalán y Carrillo, 2017; Codes y
Muñoz-Catalán, 2019; Escudero-Domínguez et al., 2019); las oportunidades de
aprendizaje; el dominio del conocimiento matemático del MTSK también en educación infantil (Martín y Carrillo, 2017); el dominio afectivo
y el MTSK (Pascual et al., 2019);
el diseño de tareas para la formación de profesores de matemáticas a partir del MTSK (Climent y Montes, 2019);
conexiones de complejización y simplificación del KMS en educación primaria
(Montañez-Esparza y Lizarde,
2019); y, el MTSK en la formación
continua de profesores de matemáticas (Quiroga y Gamboa, 2017; Valenzuela-Molina
y Ramos-Rodríguez, 2019). De este modo, es evidente que este modelo se ha ido
expandiendo en cada uno de los pensamientos de las matemáticas, como por
ejemplo el pensamiento métrico-geométrico y variacional en países como España y
Portugal en Europa, y en Brasil, México y Chile en Latinoamérica.
Conclusiones
El modelo MTSK desarrollado por Carrillo y sus
colaboradores en el año 2013, y potenciado en el año 2018 ha permitido la
caracterización del conocimiento especializado del profesor que enseña
matemáticas en cualquier nivel académico, tanto
en el conocimiento matemático, como en el didáctico-pedagógico, no evidente de manera
explícita en otros modelos que abordan el conocimiento del profesor de
matemáticas. Este modelo sustenta a través de las categorías que se presentan para cada subdominio del dominio matemático y didáctico-pedagógico,
que existen características del licenciado en matemáticas que los hace
diferenciar de otros profesionales que asumen este rol en las escuelas
colombianas, como es el caso de los ingenieros, matemáticos, estadísticos,
físicos y otro tipo de profesional con formación en matemáticas. Así mismo, se
evidenció que mediante este modelo es posible el análisis del conocimiento
especializado de los temas, de las estructuras matemáticas, prácticas
matemáticas, características de aprendizaje de las matemáticas, enseñanza de
las matemáticas y estándares de aprendizaje de las matemáticas de contenidos
particulares de las matemáticas, y que dada la amplitud del modelo permite la
relación entre estos subdominios del mismo dominio o de dominios diferentes.
Aparte, se concluye que el MTSK es una
oportunidad al estudio de una línea de investigación que relacione la formación
de profesores con el conocimiento especializado de maestros en formación
inicial, ya que mediante el análisis que se les haga a estos acerca de su
conocimiento especializado en determinado tema de las matemáticas, existe la
posibilidad de proponer planes de mejora en los programas que forman profesores
de matemáticas. Por ello este modelo es una invitación a la reflexión
del profesor en sus prácticas
matemáticas y de tipo
didáctico, ya que la misma especificidad que ofrece el MTSK, es una oportunidad para el estudio
de nuevas líneas de
investigación, como por ejemplo el estudio a profundidad del conocimiento
especializado del profesor en la enseñanza de las matemáticas en niveles de
primaria o de nivel superior utilizando las TIC escasamente abordados mediante
el modelo MTSK como referencial teórico.
De igual manera, es interesante que en Colombia se siga
profundizando en la inserción del conocimiento especializado del profesor de
matemáticas, como tema de interés a investigar en la Formación del Profesor de
Matemáticas. Esto porque consideramos que es una buena oportunidad para divulgar la necesidad que implica
en el país de que sean los licenciados en Matemáticas quienes
sean los encargados de enseñar matemáticas en las escuelas. Ya que este modelo describe
detalladamente el conocimiento con el que debe contar este tipo de
profesionales para la enseñanza de contenidos de matemáticas.
Referencias bibliogáficas
Advíncula, E., Beteta,
M., León, C., Torres, I. & Montes,
M. (2021). El conocimiento matemático del profesor acerca de la parábola: diseño de un
instrumento para su investigación. Revista Uniciencia, 35(1), 1-21. DOI:
http://dx.doi.org/10.15359/ru.35-1.12
Aguilar-González.,
Muñoz-Catalán., & Carrillo, J. (2019). An Example of Connections between
the Mathematics Teacher’s Conceptions and Specialized Knowledge. EURASIA
Journal of Mathematics, Science and Technology Education, 15(2), 1-15.
https://doi.org/10.29333/ejmste/101598
Ball, D;
Thames, M; & Phelps, G. (2008). Content Knowledge for Teaching. What makes
it Special? Journal of Teacher Education, 59(5), 389-407.
Barrera, V.,
Liñán, M., & Pérez, B. (2017). El conocimiento especializado de los
estudiantes para maestro en la resolución de problemas
de magnitudes proporcionales. Una propuesta didáctica. Actas de las III Jornadas del Seminario de Investigación de
Didáctica de la Matemática de la Universidad de Huelva, (pp. 81-85).
Huelva: CGSE
Bromme, R. (1994). Beyond Subject Matter: A Psychological
Topology of Teachers Professional Knowledge. In R. Biehler, R. Sholz, R.
Strässer, & B. Winkelman (Eds.), Didactics of Mathematics as a
Scientific Discipline (pp. 73-88). Dordrecht: Kluwer Academic Publisher.
Carrillo, J. (2019). Panorámica de la investigación con
MTSK en el mundo. IV Congreso Iberoamericano sobre Conocimiento Especializado
del Profesor de Matemáticas (7-12). Huelva: Universidad de Huelva Publicaciones.
Carrillo, J., Climent, N., Montes, M., Contreras, L., Flores, E., Escudero, D., Vasco, D.,
Rojas, N., Flores, P., Aguilar, A., Ribeiro, M., & Muñoz, M. (2018). The
mathematics teacher’s specialized knowledge (MTSK) model. Research in
Mathematics Education, 20(3), 236-253, DOI: 10.1080/14794802.2018.1479981
Carrillo, J., Climent, N., Contreras, L., & Muñoz, M. (2013).
Determining specialized knowledge
for mathematics. In Proceedings of the CERME
(Vol. 8, pp. 2985-2994)
Carrillo, J., Climent,
N., Contreras, L., & Ribero,
M. (2017). Mathematics Teacher’s Specialized Knowledge
(MTSK) in the “Dissecting an Equilateral Triangle” problem. Ripem, 7(2),
88-107.
Climent, N. (2002). El desarrollo profesional del maestro de Primaria respecto
de enseñanza de la matemática. Un estudio
de caso. Tesis doctoral. Michigan:
Proquest Michigan University.
Climent, N., &
Montes, M. (2019).
Diseño de tareas
para la formación de profesores de matemáticas a partir
de MTSK. IV Congreso Iberoamericano sobre Conocimiento Especializado del
Profesor de Matemáticas, 60-68. Huelva: Universidad de Huelva Publicaciones.
Climent, N., Espinoza-Vásquez, G., Carrillo, J.,
Henríquez-Rivas, C., & Ponce, R. (2021). Una lección sobre el teorema de Thales, vista desde el conocimiento especializado del profesor. Educación
Matemática, 33(1), 98-124.
DOI: 10.24844/EM3301.04
Codes, M., & Muñoz-Catalán, M. (2019). El uso de un vídeo de animación para promover conocimiento especializado sobre medida en estudiantes para maestro de Educación
Infantil. IV Congreso Iberoamericano sobre Conocimiento Especializado del
Profesor de Matemáticas, 201-209. Huelva: Universidad de Huelva Publicaciones
Delgado, R., & Zakaryan, D. (2019). Relationships Between the Knowledge of Practices in Mathematics and the Pedagogical Content Knowledge of a
Mathematics Lecturer. International Journal of Science and Mathematics
Education, Págs (1-21).
Escudero-Avila, D. y Carrillo, J. (2020). El Conocimiento Didáctico del Contenido: Bases teóricas y metodológicas
para
su caracterización como parte del conocimiento especializado del profesor de matemáticas. Educación
Matemática, 32(2), 8-38. DOI: 10.24844/EM3202.01
Escudero-Domínguez, A., Muñoz-Catalán,M., &
Carrillo,J. (2017). MTSK: Conocimiento especializado para la enseñanza de la geometría
en la etapa infantil. Actas de las III Jornadas
del Seminario de Investigación de Didáctica de la Matemáticas de la
Universidad de Huelva, 119-124. Huelva: CGSE
Escudero-Domínguez, A., Escudero-Ávila,D., Aguilar-González, A., & Vasco,D. (2019). El conocimiento especializado del profesor de matemáticas en Educación Infantil para la
enseñanza de geometría. IV Congreso Iberoamericano sobre Conocimiento
Especializado del Profesor de Matemáticas, 219-227. Huelva: Universidad de
Huelva Publicaciones.
Espinosa-Vásquez,G., Zakaryan,D., & Carrillo, J. (2018). El conocimiento especializado del profesor de matemáticas en el uso de la analogía en la enseñanza del concepto de función. Revista Latinoamericana de Investigación en Matemática Educativa, 21(3), 301-324.
DOI:10.12802/relime.18.2133
Fennema, E., &
Franke, M. (1992).
Teachers’ Knowledge and its impact.
In D.A. Grows
(Ed), Handbook of research
on mathematics teaching and learning: A project of the National Council of
Teachers of Mathematics (pp. 147 – 164). Macmillan Publishing Co, Inc
Flores-Medrano, E., Escudero, D., Montes, M., Aguilar,
Álvaro., & Carrillo, J. (2014). Nuestra
modelación del conocimiento especializado del profesor de matemáticas, el MTSK.
Publisher Universidad de Huelva Publicaciones. Págs (57 -72)
Flores-Medrano, E., Sosa,
L., & Ribeiro,
C. (2016). Tránsito del MKT al MTSK. Actas de la II Jornada del Seminario
de Investigación de Didáctica de la Matemática en la Universidad de Huelva.
Págs (7 -11). Huelva
Flores-Medrano, E., Montes,
M., Carrillo, J., Contreras, L., Muñoz, M., & Liñan, M. (2016).
El papel del MTSK como Modelo de Conocimiento del Profesor
en las Interrelaciones entre los Espacios de Trabajo Matemáticos. Bolema -
Mathematics Education Bulletin, 30(54), 204 -221. http://dx.doi.org/10.1590/1980- 4415v30n54a10
Martín, J., & Carrillo, J. (2017). Las oportunidades
de aprendizaje y el dominio de conocimiento matemático del MTSK en educación
infantil. Actas de las III Jornadas del Seminario de Investigación de Didáctica
de la Matemáticas de la Universidad de Huelva, 97-101. Huelva: CGS
MEN. (2016). Derechos
Básicos de Aprendizaje V.2. Bogotá: MEN
Montañez-Esparza, M., Lizarde,
E. (2019). Conexiones de simplificación y complejización en la enseñanza
de la multiplicación de fracción por natural en la escuela primaria. IV
Congreso Iberoamericano sobre Conocimiento Especializado del Profesor de
Matemáticas (149-157). Huelva: Universidad de Huelva Publicaciones.
Montes, M. (2015). Conocimiento especializado del profesor de matemáticas acerca del infinito: un estudio de caso. Universidad de Huelva, Departamento de Didáctica de las Ciencias
y la Filosofía. Tesis Doctoral
Montes, M., Aguilar, A., Escudero,
D., Moriel, J., Contreras,
L., & Climent, N. (2017). Problemas
de la Educación Matemática donde la contribución del MTSK puede
ser relevante. Actas de la III Jornada del Seminario de Investigación de Didáctica de la
Matemática en la Universidad de Huelva, Págs (68 – 70).
Montes, M., Climent,
N., Carrillo, J., & Contreras, L. (2020). Constructing tasks for primary
teacher education from the perspective of Mathematics
Teachers’ Specialised Knowledge. Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht University, Feb 2019, Utrecht,
Netherlands. hal-02430479f
Muñoz, M., & Montes, M. (2016). La investigación
sobre MTSK en las distintas etapas educativas. Actas
de la II Jornada del Seminario de Investigación de Didáctica de la Matemática en la Universidad de Huelva, Págs (87- 93). Huelva
Muñoz-Catalán,M., Liñan, M., & Ribeiro,M. (2017). Conocimiento especializado para enseñar la operación
resta en educación infantil. Cadernos de Pesquisa, 24, 4-19. http://dx.doi.org/10.18764/2178-2229. v24nespecialp4-19
Padilla-Escorcia, I., & Acevedo-Rincón, J. (2020). El
conocimiento especializado del profesor que enseña matemáticas: Mediaciones con TIC para funciones trigonométricas. Serie Educar- Editorial
Poisson, 109-118. DOI:10.36229/978-65-86127-63-8.CAP.13
Padilla-Escorcia,
I., & Acevedo-Rincón, J. (2021). Conocimiento especializado del profesor
que enseña la reflexión de la función trigonométrica seno: Mediaciones con TIC.
Eco Matemático, 12(1), 93-106. DOI 10.22463/17948231.3072
Pascual, M., Fernández-Gago, J., García, M., Marbán, J.,
& Maroto, A. (2019). El dominio afectivo y MTSK. IV Congreso Iberoamericano sobre Conocimiento Especializado del Profesor de Matemáticas, 32-40.
Huelva: Universidad de Huelva Publicaciones.
Quiroga, F., &
Gamboa, M. (2017).
Contribución del MTSK en la elaboración del plan de formación de profesores
de matemáticas. Actas de las III Jornadas del Seminario de Investigación de
Didáctica de la Matemática de la Universidad de Huelva, 125-130. Huelva: CGSE
Schoenfeld, A. (2010).
How we think. New York: Routledge.
Schön, D. (1983). The reflective
practitioner: How professionals think in action. Basic New York: Books.
Shulman, L. (1986). Those Who Understand: Knowledge
Growth in Teaching.
American Educational Research Association. Págs (4 - 14)
Valenzuela-Molina, M., & Ramos-Rodríguez, E. (2019).
IV Congreso Iberoamericano sobre Conocimiento Especializado del Profesor de
Matemáticas, 228-238. Huelva: Universidad de Huelva Publicaciones.
Vasco, D., & Climent, N. (2018). El estudio del conocimiento especializado de dos profesores
de Álgebra Lineal. PNA, Págs (129 – 146), Vol. 12(3).
Vasco, D., Climent, N., Escudero, D., Montes, M., & Ribeiro,
M. (2016). Conocimiento Especializado de
un Profesor de Álgebra Lineal
y Espacios de Trabajo Matemático. Bolema - Mathematics Education Bulletin,
Págs (222-239), Vol. 30(54).
Zakaryan, D., &
Sosa, L. (2021).
Conocimiento del profesor
de secundaria de la práctica
matemática en clases
de geometría. Educación Matemática, 33(1), 71-97. DOI:
10.24844/EM3301.03