

Revista Σοφία-SOPHIA

2025
![]()
Artículo de Investigación
![]()
Ana Milena Calabria Ramos1*![]() , Tomás José Fontalvo Herrera1
, Tomás José Fontalvo Herrera1
1Universidad de Cartagena. Cartagena, Colombia
![]()
Información del artículo Recibido: octubre de 2024 Aceptado: septiembre de 2025 Publicado: octubre de 2025
Como citar:
Calabria Ramos, A. M., Fontalvo Herrera, T.J. (2025). Implementación de curvas de operación y métricas Seis Sigma para mejorar el desempeño de un sistema productivo integrado. Sophia, 21(1).
https://revistas.ugca.edu.co/ index.php/sophia/article/vi ew/1481
Sophia-Education Copyright 2025. Universidad La
Gran Colombia
![]()
Esta obra está bajo una Licencia Attribution- ShareAlike 4.0 International
Conflicto de intereses:
Los autores declaran no tener conflictos de intereses.
*Autor para la correspondencia: acalabriar@unicartagena.edu.co
![]()
ABSTRACT This research addresses the application of the Six Sigma methodology in an integrated production system with the aim of improving its performance. This paper highlights the importance of optimizing production processes to reduce defects and increase operational efficiency in a competitive environment. The main objective is to analyze how Six Sigma can reduce defects per million opportunities (DPMO) and improve the Sigma level in each process. The methodology used includes a quantitative analysis of production data and the implementation of Six Sigma metrics, evaluating the results through operating curves that show performance according to the Sigma level. The results indicate a significant reduction in defects in all the processes analyzed, with an improvement in the overall performance of the system.
![]()
Finally, it is underlined that the implementation of Six Sigma is effective in optimizing quality and efficiency in complex production systems, achieving a Sigma level that reduces defects to almost zero, improving competitiveness and reducing operating costs
![]()
![]()
En la era de la globalización, donde la competencia industrial es cada vez más feroz, las empresas no solo deben centrarse en satisfacer las demandas de los consumidores, sino también en optimizar sus procesos internos para maximizar la eficiencia y reducir al mínimo los defectos en la producción. Por consiguiente, la metodología Seis Sigma se ha consolidado como una de las herramientas más potentes en la búsqueda de la excelencia operativa, proporcionando un marco que permite a las organizaciones reducir la variabilidad en sus procesos aparte del hecho de mejorar la calidad de sus productos o servicios (Aizaga, 2022).
El enfoque de Seis Sigma se basa en la premisa que, si un proceso se gestiona adecuadamente, el número de defectos por cada millón de oportunidades (DPMO, por sus siglas en inglés) tiende a reducirse hasta niveles insignificantes, alcanzando una meta de solo 3.4 defectos por millón de unidades producidas (Victorio, 2020). Debido a ello, este estándar de calidad, cuando se aplica correctamente, tiene un impacto directo en la rentabilidad, ya que menos productos defectuosos se traducen en menores costos de reprocesamiento, menores tasas de devoluciones y una mayor
![]()
satisfacción del cliente. A pesar de ello, el camino para implementar Seis Sigma en un sistema productivo integrado requiere un conocimiento de los principios teóricos que sustentan la metodología, aparte de su aplicación práctica en el contexto específico de cada industria.
De acuerdo con Simón (2024), el sistema productivo integrado que se aborda en esta investigación comprende una red compleja de procesos interrelacionados, donde cualquier variabilidad en una etapa del proceso puede tener un efecto dominó en las etapas posteriores. En este sentido, la optimización de la calidad no puede lograrse sin una evaluación absoluta del sistema en su conjunto, utilizando herramientas estadísticas avanzadas que permitan la identificación de cuellos de botella, la medición precisa del rendimiento y la construcción de curvas de operación que faciliten la toma de decisiones estratégicas. Por ello, las curvas de operación, en particular, desempeñan un papel crucial en la evaluación del desempeño del sistema, ya que permiten visualizar las probabilidades de aceptación de lotes en función de la fracción defectuosa, proporcionando una representación gráfica que facilita la identificación de riesgos en el muestreo (Irigoin et al., 2023).
Cabe destacar que, un aspecto en la implementación de Seis Sigma es el enfoque en la mejora continua, donde se busca corregir los errores existentes, aparte de anticipar problemas potenciales antes de que estos se manifiesten en el sistema productivo. Por ello, la metodología se basa en el uso de datos cuantitativos y análisis estadísticos rigurosos que permitan a las organizaciones establecer estándares de calidad más altos que, al mismo tiempo, desarrollar una cultura organizacional orientada a la mejora constante (Franco, 2021). Debido a ello, esto implica un cambio de mentalidad en todos los niveles de la organización, desde la alta dirección hasta los operarios en planta, quienes deben estar alineados con los objetivos de calidad y comprometidos con la reducción de la variabilidad en los procesos.
En este contexto, el uso de métricas de Seis Sigma resulta fundamental para evaluar el desempeño de un sistema productivo integrado, puesto que, estas métricas incluyen el nivel sigma (Z), que mide la capacidad del proceso para producir resultados dentro de los límites especificados, que evalúa qué tan centrado está el proceso en comparación con los límites de especificación (Fontalvo, 2024). A través de estas métricas, es posible determinar la calidad del sistema en un momento dado, para también predecir cómo se comportará el sistema bajo diferentes condiciones de operación, de modo que, la construcción de curvas de operación para cada uno de los procesos del sistema permite una evaluación más detallada, identificando qué procesos son más susceptibles a variabilidad y cuáles son más estables.
![]()
En la presente investigación, se aplicarán las métricas de Seis Sigma y las curvas de operación a un sistema productivo integrado, con el fin de mejorar su rendimiento junto con el hecho de reducir el número de productos defectuosos. El análisis se enfocará en la optimización del flujo de materiales a través de los diferentes puntos de proceso, evaluando cómo los cambios en el nivel sigma (Z) pueden afectar el rendimiento global del sistema.
La implementación de Seis Sigma en un sistema productivo integrado no es una tarea sencilla, ya que requiere un compromiso total por parte de la organización y un enfoque riguroso en la recolección y análisis de datos. Aunque, los beneficios potenciales de este enfoque son significativos, ya que no solo se mejora la calidad de los productos, sino que también se incrementa la eficiencia operativa y se reducen los costos asociados con la producción defectuosa. En un entorno donde la presión por reducir costos aparte de aumentar la competitividad es cada vez mayor, la adopción de metodologías como Seis Sigma se presenta como una estrategia clave para lograr el éxito a largo plazo (Guerrero et al., 2019).
En este contexto, se plantean las siguientes interrogantes que guiarán esta investigación:
¿Cómo evaluar el desempeño de un sistema productivo integrado utilizando métricas Seis Sigma?,
¿Cómo optimizar el nivel Sigma (Z) para reducir la cantidad de defectos en un sistema de producción?, ¿De qué manera pueden construirse curvas de operación que reflejen la eficiencia de los procesos productivos?, ¿Cómo determinar el nivel Sigma adecuado para minimizar los errores en el sistema?, ¿Cuál es el impacto de las variaciones en el nivel Sigma en la calidad general del sistema?
Para dar respuesta a estas preguntas, el objetivo general de esta investigación es proponer un marco de mejora basado en la metodología Seis Sigma que permita optimizar el desempeño de un sistema productivo integrado, reduciendo significativamente los defectos y mejorando la eficiencia operativa. Por otro lado, los objetivos específicos se desglosan de la siguiente manera. 1) Evaluar el sistema productivo integrado utilizando indicadores de Seis Sigma, determinando el nivel Sigma de cada proceso. 2) Desarrollar curvas de operación para analizar el desempeño del sistema productivo global y los procesos individuales. 3) Determinar los valores óptimos de Sigma que minimicen los defectos en el sistema. 4) Proponer estrategias de mejora para optimizar el nivel Sigma (Z) y reducir el número de productos defectuosos (n). 5) Elaborar una curva de rendimiento promedio de corrida (RPC) para visualizar las variaciones en el nivel Sigma a lo largo del tiempo.
![]()
Revisión de la literatura
En la actualidad, las empresas enfrentan el reto constante de mejorar la calidad y eficiencia de sus procesos productivos. La metodología Seis Sigma ha emergido como una herramienta clave para lograr altos niveles de desempeño en sistemas productivos complejos. A través de su enfoque en la reducción de la variabilidad junto al control riguroso de los defectos, Seis Sigma permite a las organizaciones optimizar sus procesos y alcanzar estándares de calidad cada vez más exigentes. Por ello, este apartado aborda los conceptos fundamentales relacionados con el sistema de medición Seis Sigma, las curvas de operación de sus métricas, la evaluación de la calidad en un sistema productivo, aparte de cómo estas métricas se aplican en la evaluación de un sistema integrado productivo.
Sistema de medición Seis Sigma
El sistema de medición Seis Sigma es una metodología basada en el análisis estadístico que permite identificar, cuantificar y minimizar la variabilidad en los procesos productivos, de modo que, este sistema se basa en la premisa de que todo proceso tiene inherentemente cierto grado de variación; en contraste, es posible controlarla para alcanzar niveles de calidad superiores (Garza et al., 2016). El término “sigma” hace referencia a una medida de desviación estándar, utilizada para representar la variabilidad en un conjunto de datos. Un proceso que opera en niveles de Seis Sigma tiene una variabilidad tan baja que produce solo 3.4 defectos por millón de oportunidades (DPMO), lo que significa que el margen de error es prácticamente insignificante (Marin et al., 2022).
Según Garza et al., (2016), la implementación de un sistema de medición Seis Sigma involucra el uso de herramientas estadísticas avanzadas para analizar los procesos, entre estas herramientas, se destaca el ciclo DMAIC (Definir, Medir, Analizar, Mejorar y Controlar), un enfoque sistemático que guía a las organizaciones en la identificación de problemas, medición de variables críticas, análisis de causas raíz, mejora de los procesos y control de los resultados a largo plazo, puesto que, este enfoque estructurado es esencial para garantizar que los esfuerzos de mejora se mantengan sostenibles y generen un impacto duradero en el sistema productivo.
En un sistema productivo integrado, el uso de Seis Sigma permite evaluar el desempeño de procesos individuales, aparte del rendimiento del sistema en su conjunto (Jurado, 2019). Las métricas clave utilizadas en este sistema de medición incluyen el índice de capacidad, que mide qué tan centrado y estable está un proceso en comparación con los límites de especificación, y el nivel sigma
![]()
(Z), que indica la calidad general del proceso, ya que, estas métricas proporcionan una base sólida para evaluar la eficacia del sistema y guiar la toma de decisiones estratégicas para su optimización.
Curvas de operación de métricas Seis Sigma
Las curvas de operación constituyen una herramienta visual fundamental en la aplicación de Seis Sigma, ya que permiten evaluar el desempeño de un proceso en términos de probabilidad de aceptación de lotes en función de la fracción defectuosa (Fontalvo, 2024). Por ello, estas curvas son esenciales para la toma de decisiones en el control de calidad, ya que proporcionan una representación gráfica que facilita la identificación de riesgos en el muestreo junto a la evaluación de la eficiencia del sistema.
Cabe mencionar que, en un contexto de Seis Sigma, las curvas de operación permiten visualizar cómo un cambio en los parámetros del proceso, como el nivel sigma, puede afectar la probabilidad de que un lote sea aceptado o rechazado, es particularmente relevante en sistemas productivos integrados, donde múltiples procesos interrelacionados deben ser coordinados para garantizar que los productos cumplan con los estándares de calidad establecidos. Al utilizar las curvas de operación, es posible identificar qué procesos dentro del sistema son más propensos a la variabilidad y requieren mayor atención, aparte de los cuales operan de manera eficiente con un bajo nivel de defectos (Gutierrez, 2019).
Por otro lado, las curvas de operación son útiles para establecer puntos de control en el proceso productivo, lo que permite a las organizaciones predecir y prevenir problemas antes de que estos afecten la calidad final del producto. Ahora bien, al implementar Seis Sigma en un sistema productivo integrado, las curvas de operación se convierten en una herramienta esencial para gestionar la variabilidad y garantizar que todos los procesos operen dentro de los límites aceptables (Ortiz, 2020).
Evaluación de la calidad en un sistema productivo
La evaluación de la calidad en un sistema productivo integrado requiere un enfoque integral que considere tanto los procesos individuales como su interacción dentro del sistema, puesto que, seis Sigma ofrece un marco robusto para esta evaluación, basado en la medición y control de la variabilidad en cada etapa del proceso. La calidad se evalúa en términos de defectos por millón de oportunidades (DPMO), nivel sigma, y la capacidad del proceso para producir resultados dentro de los límites de especificación (Salazar, 2019).
![]()
Uno de los aspectos clave de la evaluación de la calidad en un sistema productivo es la identificación de las variables críticas que afectan el desempeño del sistema, debido a ello, estas variables, también conocidas como CTQ (Critical to Quality), son los factores que tienen un impacto directo en la calidad del producto o servicio final (Fleaca, 2019).
En un sistema productivo integrado, la evaluación de la calidad debe ir más allá de la simple identificación de defectos, de modo que, es fundamental entender cómo los diferentes procesos interactúan entre sí y cómo las mejoras en un proceso pueden afectar el rendimiento de todo el sistema. El uso de métricas de Seis Sigma permite a las organizaciones medir no solo el desempeño de procesos individuales, sino también el impacto global de las mejoras en el sistema.
Métricas Seis Sigma para evaluar un sistema integrado productivo
En un sistema integrado productivo, las métricas de Seis Sigma proporcionan una herramienta poderosa para evaluar el rendimiento del sistema junto con el hecho de guiar los esfuerzos de mejora continua (Estrella, 2022). Las métricas más comúnmente utilizadas incluyen el nivel sigma (Z) y los defectos por millón de oportunidades (DPMO), ya que, estas métricas ofrecen una visión detallada del desempeño del sistema, permitiendo a los gestores identificar áreas de oportunidad aparte de establecer objetivos de mejora.
El nivel sigma (Z) es quizás la métrica más representativa de la metodología Seis Sigma, ya que mide cuán bien se está ejecutando un proceso en relación con los límites de especificación establecidos (Fernández et al., 2020). En un sistema productivo integrado, es crucial que todos los procesos operen en niveles de sigma altos para garantizar que el sistema en su conjunto cumpla con los estándares de calidad. Un nivel sigma bajo en uno de los procesos puede afectar negativamente el rendimiento de todo el sistema, lo que subraya la importancia de utilizar estas métricas para monitorear y optimizar cada etapa del proceso productivo.
El desarrollo de esta investigación se centra en analizar el desempeño del sistema productivo integrado mediante la aplicación de Seis Sigma, se adoptó un enfoque cuantitativo basado en la recolección y análisis de datos de procesos productivos clave, debido a ello, este sistema asignado consta de múltiples fases de producción, cada una de las cuales fue evaluada utilizando las métricas de Seis Sigma para identificar oportunidades de mejora en términos de eficiencia y calidad. A lo largo
![]()
del proceso, se aplicaron técnicas estadísticas avanzadas para analizar la variabilidad del sistema y reducir los defectos (Figura 1).
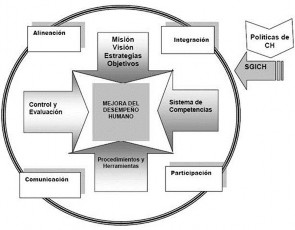
Figura 1. - Método sistemático de evaluación del desempeño para el sistema integrado
El sistema productivo evaluado está compuesto por ocho procesos principales que trabajan de manera interrelacionada, de modo que, estos métodos fueron estudiados bajo el esquema de Seis Sigma, con un enfoque en la optimización del flujo de materiales y la reducción de defectos a lo largo del sistema (Bonilla, 2020). La identificación de entradas y salidas en cada proceso fue clave para modelar el sistema y entender cómo las métricas de Seis Sigma podrían ser aplicadas para medir el rendimiento (Figura 2).
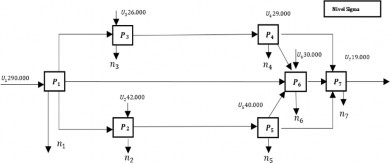
Figura 2. - Diagrama del sistema productivo
![]()
Por otro lado, mediante lo establecido en las métricas Seis Sigma, se da de forma descriptiva en lo correspondiente a la Tabla 1, la realización de la examinación correspondiente al proceso de rendimiento productivo; que permite lo correspondiente a una perspectiva lógica de carácter preciso para establecer la práctica de forma colectiva y personal, por medio del cual se atestigua la apreciación más confidencial en cláusulas de disposición y validez.
Tabla 1. - Métricas Seis Sigma
Métricas | Definición |
DPMO | Cantidad de defectos de partes por millón |
Z | Nivel Sigma |
Y | Rendimiento del proceso |
U | Cantidad de unidades entrantes |
O | Oportunidad de error |
T | Total de defectos (UxO) |
n | Número de no conformidades |
S | Salida de unidades (U-n) |
Fuente: elaboración propia.
El siguiente paso en la metodología fue la implementación de las métricas de Seis Sigma. Estas métricas proporcionaron una base sólida para evaluar el desempeño individual y global del sistema productivo. Ahora bien, entre las principales métricas utilizadas se encuentran los Defectos por Millón de Oportunidades (DPMO), el Nivel Sigma (Z), y el Rendimiento del Proceso (Y) (Tolagasí, 2018). Por consiguiente, se calculó el DPMO global del sistema utilizando la Fórmula 1.
𝟐𝟗.𝟑−(𝒛−𝟎.𝟖𝟒𝟎𝟔)𝟐
![]()
[
𝑫𝑷𝑴𝑶 = 𝒆
𝟐.𝟐𝟐𝟏 ] (1)
Este valor permitió evaluar el nivel de calidad del sistema productivo en su conjunto. Una vez calculado el DPMO global, se determinó la cantidad de prendas defectuosas en cada uno de los procesos. Para ello, se utilizó la siguiente Fórmula 2:
𝒏𝒈
= 𝑫𝑷𝑴𝑶∗𝑼∗𝑶
![]()
𝟏.𝟎𝟎𝟎.𝟎𝟎𝟎
(2)
Donde 𝑛𝑔 representa la cantidad total de partes rechazadas por todo el sistema productivo, 𝑈 es la cantidad de unidades de entrada, y 𝑂 corresponde a la oportunidad de error por unidad. De esta manera, se cuantificaron los defectos en cada una de las fases de producción.
![]()
A lo largo del estudio, se evaluaron las salidas de cada proceso y se descontaron las prendas defectuosas antes de avanzar al siguiente proceso, debido a ello, este análisis permitió calcular las DPMO específicas para cada fase de producción. Posteriormente, se calcularon los niveles Sigma individuales de cada proceso utilizando la siguiente Fórmula 3:
![]()
𝑍 = √29.3 − 2.221 ∗ ln (𝐷𝑃𝑀𝑂) + 0.8406 (3)
Este cálculo fue crucial para determinar el desempeño individual de cada proceso dentro del sistema. La construcción de las curvas de operación ayudó a visualizar el rendimiento de cada etapa del sistema productivo, permitiendo identificar los procesos que generaban mayor variabilidad y los que operaban de manera más eficiente.
El rendimiento de cada proceso se puede determinar con la Fórmula 4:
![]()
Y = 1 − 𝑛 (4)
𝑈
Lo que da como resultado el porcentaje de unidades conformes que salen de cada proceso. Dado que el sistema incluye procesos paralelos, es importante combinar los rendimientos de
𝑃2, 𝑃3, 𝑃4, 𝑃5, 𝑃6 antes de llegar al proceso final. 𝑃7 Las ecuaciones específicas para calcular la entrada/salida neta de cada proceso serían similares a la Fórmula 5.
𝑈6 = (𝑈2 − 𝑛2) + (𝑈3 − 𝑛3) + 2 (𝑈4 − 𝑛4) (5)
𝑈7 = (𝑈6 − 𝑛6) + (𝑈5 − 𝑛5)
Uno de los objetivos principales de este estudio fue optimizar el nivel sigma (Z) del sistema productivo. En este sentido, se realizó un análisis de sensibilidad para evaluar cómo diferentes niveles de Z impactaban el rendimiento del sistema, de modo que, se definió un rango de niveles sigma permisibles entre 3.0 y 4.5, en consonancia con los estándares de calidad establecidos.
Para cada nivel sigma, se generaron diferentes escenarios de simulación que permitieron observar cómo se comportaba el sistema productivo bajo diferentes condiciones de operación, puesto que, este análisis permitió identificar los puntos de mejora críticos dentro del sistema aparte del hecho de proporcionar recomendaciones específicas para reducir la variabilidad y aumentar la eficiencia.
El uso de las métricas Seis Sigma fue clave para guiar las decisiones en la optimización del sistema productivo, por su parte, mediante el análisis de las salidas de cada proceso, se pudo cuantificar de manera precisa el impacto de las mejoras implementadas, lo que permitió ajustar los procesos en tiempo real y reducir significativamente los niveles de defectos (Tabla 2).
![]()
Tabla 2. - Criterios de desempeño para el sistema de prestación de servicios
Nivel Sigma (Z) | Desempeño |
Z < 3,0 | Deficiente |
3,0 ≤ Z ≤ 3,5 | Aceptable |
3,5 < Z ≤ 4,6 | Sobresaliente |
Z > 4,6 | Excelente |
Fuente: elaboración propia.
El análisis metodológico desarrollado a lo largo de este artículo permitió obtener una visión clara y cuantitativa del desempeño del sistema productivo integrado. La implementación de las métricas Seis Sigma y el uso de curvas de operación y de rendimiento promedio de corrida proporcionaron una base sólida para la toma de decisiones, guiando el proceso de optimización y reducción de defectos, aparte de ello, este enfoque permitió mejorar significativamente el nivel sigma del sistema productivo, contribuyendo a un aumento en la eficiencia global y una reducción en la variabilidad de los procesos.
El presente apartado detalla los resultados obtenidos tras la implementación de la metodología Seis Sigma en un sistema productivo integrado, con base en la aplicación de diversas métricas clave para medir el rendimiento y la calidad del sistema. Por consiguiente, estas métricas incluyen el Nivel Sigma (Z), los Defectos por Millón de Oportunidades (DPMO), el rendimiento (Y) debido a ello, la cantidad de productos defectuosos (n). A lo largo de los ocho procesos clave que componen el sistema, se observó una notable variabilidad en los resultados, lo que permitió identificar áreas críticas de mejora, así como procesos con un desempeño sobresaliente.
Siguiendo el modelo planteado en la metodología, se dio paso a evaluar el funcionamiento del sistema productivo integrado utilizando las métricas Seis Sigma, obteniendo los siguientes resultados (Tabla 3).
![]()
Tablas de resultado de las métricas de Seis Sigma aplicadas a cada uno de los procesos del sistema productivo integrado
Tabla 3. - Valores mínimos y máximos para cada proceso de acuerdo a las métricas Seis Sigma
Valores mínimo y máximo para cada proceso | ||||||||||
Mínimos | Máximos | |||||||||
Procesos | Z | DPMO | n | Y | Desempeño | Z | DPMO | n | Y | Desempeño |
Proceso Global | 3 | 65.693 | 31.270 | 93,43 % | Deficiente | 6 | 3 | 2 | 100 % | Excelente |
Proceso 1 | 3,88 | 8.294 | 2.405 | 99,17 % | Sobresaliente | 6,43 | 0 | 0 | 100 % | Excelente |
Proceso 2 | 3,30 | 34.894 | 4.811 | 96,51 % | Aceptable | 6,14 | 1,77 | 0 | 100 % | Excelente |
Proceso 3 | 3,25 | 39.476 | 4.811 | 96,05 % | Aceptable | 6,11 | 2,00 | 0 | 100 % | Excelente |
Proceso 4 | 3,50 | 21.958 | 3.207 | 97,80 % | Aceptable | 6,24 | 1,08 | 0 | 100 % | Excelente |
Proceso 5 | 3,57 | 18.532 | 3.207 | 98,15 % | Sobresaliente | 6,27 | 0,91 | 0 | 100% | Excelente |
Proceso 6 | 3,77 | 11.364 | 3.207 | 98,86 % | Sobresaliente | 6,37 | 0,56 | 0 | 100 % | Excelente |
Proceso 7 | 3,52 | 21.176 | 9.621 | 97,88 % | Sobresaliente | 6,25 | 1,03 | 0 | 100 % | Excelente |
Fuente: elaboración propia
Evaluación del nivel Sigma (Z)
El análisis de los resultados obtenidos mediante la aplicación de la metodología Seis Sigma al sistema productivo integrado revela hallazgos significativos que ilustran la evolución de la calidad en los procesos, la eficiencia operativa y el impacto de las intervenciones en los niveles de defectos. A través del estudio de las curvas de operación para cada nivel Sigma (Z), se ha logrado identificar patrones de comportamiento y oportunidades de mejora que consolidan la estrategia implementada para la optimización del sistema.
Análisis de las curvas de operación de defectos por millón de oportunidades (DPMO)
El comportamiento de los defectos por millón de oportunidades (DPMO) en relación con los niveles Sigma fue documentado mediante ocho curvas de operación. Cada gráfico corresponde a uno de los principales procesos del sistema productivo, permitiendo visualizar la evolución de los defectos a medida que el nivel Sigma aumenta, puesto que, se observó una tendencia positiva, en la que un incremento en los valores de Z reduce el número de defectos.
Conviene destacar que, en el Proceso 1, con un nivel Sigma inicial de 3.88, se reportaron 2405 defectos en un universo de 290.000 unidades, lo que equivalía a un DPMO de 8.294. Sin embargo, a medida que el nivel Sigma aumentó a 6.43, el número de defectos fue prácticamente eliminado,
![]()
alcanzando un DPMO de 0, lo que indica que el proceso se encontraba en un nivel de calidad excelente, con una eficiencia del 100%. Por ello, se replica en varios de los procesos analizados, como se observa en los gráficos de operación del Proceso 6, donde se registró un DPMO inicial de 11.364 en un nivel Sigma de 3.77 y se redujo a 0 con un Sigma de 6.37.
Las curvas de operación permiten evaluar el impacto directo de la mejora de los niveles Sigma sobre la cantidad de defectos y la eficiencia operativa de cada proceso. Ahora bien, al aplicar estas métricas, se confirma que, a partir de un nivel Sigma de 4.5, la disminución de defectos se hace mucho más notoria, destacando la importancia de alcanzar junto con el hecho de superar este umbral en los procesos para lograr un sistema productivo altamente eficiente.
Rendimiento del sistema global
El análisis del rendimiento global del sistema (Yg) reveló un comportamiento altamente positivo en función del incremento del nivel Sigma. A nivel inicial, con un Sigma de 3.0, el rendimiento era del 93,43%, con 31.270 defectos sobre un total de 476.000 unidades procesadas, lo que correspondía a un DPMO de 65.693. Por otro lado, a medida que se implementaron mejoras y el nivel Sigma se incrementó progresivamente, el rendimiento del sistema mostró una mejora sustancial.
En niveles Sigma de 4.2, el rendimiento global alcanzó el 99.67%, con un DPMO reducido a 3.331, lo que evidenció una optimización significativa del sistema productivo, puesto que, al alcanzar un Sigma de 6.0, el rendimiento del sistema llegó al 100%, eliminando prácticamente todos los defectos, lo que demuestra el éxito de las estrategias implementadas para la mejora continua, debido a ello, este nivel de calidad refuerza el enfoque Seis Sigma como una herramienta esencial para la gestión eficiente de la producción, asegurando productos libres de defectos y minimizando los reprocesos.
Análisis - curvas de operación de defectos por millón de oportunidades (DPMO) para cada nivel Sigma (Z)
La aplicación de la metodología Seis Sigma en el sistema productivo integrado ha permitido evaluar el rendimiento del proceso mediante métricas clave como los Defectos por Millón de Oportunidades (DPMO), el Nivel Sigma (Z) y el rendimiento del proceso (Y). Debido a ello, el análisis de estos resultados ha facilitado la identificación de áreas críticas que requieren intervención, sino
![]()
que también ha revelado los puntos de fortaleza dentro del sistema, donde la calidad es alta y el control de la variabilidad ha sido efectivo.
El análisis individual de los procesos ofrece una visión detallada de las particularidades de cada fase productiva, revelando tanto las áreas de mejora como los puntos fuertes del sistema. El Proceso 1, uno de los más destacados, mostró una reducción constante de defectos a medida que aumentaba el nivel Sigma. Desde un DPMO inicial de 8.294 con un Sigma de 3.88, el proceso evolucionó hasta eliminar completamente los defectos con un Sigma de 6.43, lo que permitió alcanzar un rendimiento del 100% (Tabla 4).
Tabla 4. - Defectos por millón de oportunidades (DPMO) a reducir por cada Z para pasar de Z₁ a Z₂
Procesos | Z₁ | Z₂ | Reducir |
Global | 65693 | 22202 | 43491 |
1 | 8294 | 2803 | 5491 |
2 | 34894 | 11747 | 23146 |
3 | 39476 | 13283 | 26192 |
4 | 21958 | 7237 | 14721 |
5 | 18532 | 6131 | 12401 |
6 | 11364 | 3755 | 7606 |
7 | 21176 | 6937 | 14238 |
Fuente: elaboración propia
De manera similar, los procesos 2 y 3, que comenzaron con altos niveles de defectos (DPMO de 34.894 y 39.476, respectivamente), mostraron mejoras significativas tras la implementación de las estrategias de mejora de Seis Sigma. Por consiguiente, estos procesos, que inicialmente operaban con niveles Sigma cercanos a 3.3, lograron disminuir sus defectos hasta alcanzar DPMO cercanos a 0 cuando se alcanzaron niveles Sigma superiores a 5.75.
A pesar de ello, estos resultados también destacan la variabilidad inicial entre los diferentes procesos, mientras que algunos alcanzaron niveles Sigma de 6.0 rápidamente, otros, como el Proceso 7, requirieron más tiempo para alcanzar ese nivel de excelencia, debido a un mayor número de productos defectuosos al inicio del análisis. Aunque, al final del estudio, todos los procesos lograron acercarse a un rendimiento del 100%, consolidando el éxito global de la intervención.
![]()
Análisis - curvas de operación de no conformidades (n) para cada nivel Sigma (Z)
A nivel global, el sistema productivo mostró una correlación directa entre el nivel Sigma y la cantidad de defectos por millón de oportunidades (DPMO). Al inicio del análisis, con un nivel Sigma de 3.0, el sistema presentó un rendimiento global del 93.43%, con un total de 31.270 defectos. A medida que se implementaron mejoras y el nivel Sigma aumentó, el rendimiento mejoró de manera exponencial. Con un Sigma de 5.6, el rendimiento global alcanzó el 100%, con un DPMO de solo 20, lo que implica que prácticamente se eliminaron los defectos en la producción. Debido a ello, estos resultados reflejan la importancia de aumentar los niveles Sigma para lograr un sistema productivo de alta calidad. Por otra parte, se destacan la efectividad de Seis Sigma como metodología para identificar y corregir las fuentes de variabilidad en los procesos, permitiendo una mejora continua y sostenida en el tiempo (Tabla 5).
Tabla 5. - No conformidades (n) a reducir por cada Z para pasar de Z₁ a Z₂
Procesos | Z₁ | Z₂ | Reducir |
Global | 31270 | 10568 | 20702 |
1 | 2405 | 813 | 1592 |
2 | 4811 | 1626 | 3185 |
3 | 4811 | 1626 | 3185 |
4 | 3207 | 1084 | 2123 |
5 | 3207 | 1084 | 2123 |
6 | 3207 | 1084 | 2123 |
7 | 9621 | 3252 | 6369 |
Fuente: elaboración propia
El análisis de los resultados del sistema productivo integrado, evaluado bajo la metodología Seis Sigma, ofrece una visión clara de la evolución de los defectos por millón de oportunidades (DPMO) a medida que se incrementa el nivel Sigma (Z) en cada uno de los procesos del sistema. Cabe mencionar que, las curvas de operación construidas permiten visualizar cómo los diferentes niveles de Sigma impactan directamente en la cantidad de no conformidades (n) en cada etapa, proporcionando información valiosa para la toma de decisiones estratégicas de mejora continua.
![]()
Proceso global
En el análisis del sistema productivo global, se evidenció una reducción progresiva en la cantidad de no conformidades (n) conformes el nivel Sigma alcanzó valores superiores. En el nivel Sigma 3.0, el sistema presentó 31.270 no conformidades, lo que equivale a un DPMO de 65.693 y un rendimiento del 93,43%. A pesar de ello, conforme se implementaron mejoras y se elevó el nivel Sigma, el sistema mostró una disminución significativa de los defectos. Con un nivel Sigma de 5.1, las no conformidades se redujeron a 72, con un DPMO de 152 y un rendimiento cercano al 100%. En definitiva, al alcanzar un Sigma de 6.0, se observó la eliminación casi total de los defectos, con solo 2 no conformidades y un rendimiento del 100%.
Por consiguiente, este comportamiento refuerza la relación inversa entre el nivel Sigma y la cantidad de defectos, a medida que el nivel Sigma aumenta, los defectos por millón de oportunidades disminuyen exponencialmente. Debido a ello, esta tendencia es clave para justificar las inversiones en mejoras continuas dentro de los sistemas productivos, ya que los beneficios de elevar los niveles Sigma se traducen en productos de mayor calidad y una disminución significativa de costos asociados a los defectos.
Proceso 1
El proceso uno, con un nivel Sigma inicial de 3.88, comenzó con un total de 2.405 no conformidades, lo que se tradujo en un DPMO de 8.294 y un rendimiento del 99,17%, a pesar de ello, a medida que el nivel Sigma se incrementó a 5.61, las no conformidades disminuyeron considerablemente a 6, y con un Sigma de 6.43, se lograron eliminar completamente los defectos, con un rendimiento perfecto del 100%. Ahora bien, este proceso destaca por su evolución favorable a lo largo del tiempo, donde la optimización de los procedimientos y controles internos permitió una mejora sustancial en la calidad del producto final. La curva de operación muestra que a partir de un Sigma de 4.5, la cantidad de defectos se reduce de manera más acelerada, lo que sugiere que este es un umbral clave para garantizar una disminución drástica de las no conformidades.
Proceso 2
En el proceso dos, que partió de un nivel Sigma de 3.30, se reportaron inicialmente 4.811 no conformidades, lo que representaba un DPMO de 34.894,65 y un rendimiento del 96,51%, puesto que, este proceso presentó una mejora considerable con el tiempo. A un nivel Sigma de 5.75, las no
![]()
conformidades se redujeron a uno, con un rendimiento del 100%, lo que refleja una mejora total en la calidad. Por otra parte, este proceso, que comenzó con uno de los niveles Sigma más bajos del sistema, mostró la mayor variabilidad en términos de calidad, aunque, gracias a la implementación de estrategias de mejora continua, logró superar los niveles críticos de defectos. La curva de operación correspondiente a este proceso muestra una tendencia descendente clara en las no conformidades a medida que el nivel Sigma aumenta, lo que evidencia el impacto positivo de las mejoras.
Proceso 3
El proceso tres presentó una situación similar a la del Proceso 2. Con un Sigma inicial de 3.25, el proceso arrancó con 4.811 no conformidades y un DPMO de 39.476,08, en contraste, gracias a los ajustes implementados, el proceso alcanzó un nivel Sigma de 6.11, lo que eliminó los defectos por completo, con un rendimiento del 100%. Por su parte, este proceso mostró una curva de operación con una caída constante de los defectos, lo que reafirma la eficacia del enfoque Seis Sigma en la estabilización de procesos productivos complejos. A partir de un Sigma de 4.8, las mejoras se tornan más evidentes, con una reducción significativa en la cantidad de no conformidades.
Proceso 4
En el caso del proceso cuatro, el análisis mostró que con un Sigma de 3.50, el número de no conformidades era de 3.207, lo que correspondía a un DPMO de 21.958,74. Conforme el nivel Sigma se incrementó a 6.24, el proceso logró eliminar los defectos por completo, con un rendimiento del 100%. Debido a ello, la curva de operación para este proceso indica que las mejoras fueron más graduales, con una caída menos pronunciada en comparación con otros procesos, ya que, esto podría sugerir la necesidad de optimizar aún más los controles internos y las fases de inspección para garantizar una reducción más rápida de los defectos en futuros ciclos de mejora.
Proceso 5
El proceso cinco inició con 3.207 no conformidades y un DPMO de 18.532,73, con un nivel Sigma de 3.57. A medida que el proceso alcanzó un nivel Sigma de 5.89, las no conformidades se redujeron a 1, lo que nuevamente demuestra el impacto de la metodología Seis Sigma en la calidad del producto. De modo que, la curva de operación de este proceso es notablemente similar a la de los otros procesos que iniciaron con un nivel Sigma bajo, mostrando una caída significativa en la cantidad de no conformidades a medida que el nivel Sigma supera 4.5.
![]()
Procesos 6 y 7
El proceso seis, que comenzó con un Sigma de 3.77 y 3.207 no conformidades, y el proceso siete, que inició con un Sigma de 3.52 y 9.621 no conformidades, mostraron patrones similares. Ambos procesos alcanzaron un rendimiento del 100% cuando se elevaron a un Sigma superior a 6.0. En particular, las curvas de operación para estos procesos reflejan la importancia de mantener un nivel Sigma elevado para garantizar una producción libre de defectos.
A partir de un Sigma de 5.0, se observaron reducciones importantes en las no conformidades, lo que respalda la eficacia de los métodos implementados. Debido a esto, el sistema global logró una reducción significativa en la cantidad de no conformidades, pasando de 31.270 defectos con un Sigma de 3.0 a solo 2 defectos con un Sigma de 6.0, ya que, este éxito subraya la importancia de aplicar la metodología Seis Sigma de manera consistente para garantizar procesos productivos eficientes y de alta calidad.
Análisis - curvas de operación de porcentaje de rendimiento (Y) para cada nivel Sigma (Z)
El análisis de los resultados obtenidos tras la implementación de la metodología Seis Sigma en el sistema productivo integrado revela una tendencia significativa hacia la mejora continua y la reducción de defectos, debido a ello, este apartado examina los datos a través de las curvas de operación que ilustran el comportamiento de los defectos por millón de oportunidades (DPMO) y el porcentaje de rendimiento (Y) en función de los diferentes niveles Sigma (Z) alcanzados en cada proceso. Por consiguiente, la correlación entre el incremento del nivel Sigma y la mejora en la eficiencia operativa es clara, permitiendo obtener una producción más consistente y libre de defectos (Tabla 6)
![]()
Tabla 6. - Rendimiento (Y) a aumentar por cada Z para pasar de Z₁ a Z₂.
Procesos | Z₁ | Z₂ | Reducir |
Global | 93.43 | 97.78 | 4.3499 |
1 | 99.17 | 99.72 | 0.5499 |
2 | 96.51 | 98.83 | 2.3199 |
3 | 96.05 | 98.67 | 2.6200 |
4 | 97.8 | 99.28 | 1.4800 |
5 | 98.15 | 99.39 | 1.2399 |
6 | 98.86 | 99.62 | 0.7600 |
7 | 97.88 | 99.31 | 1.4300 |
Fuente: elaboración propia
Análisis de los curvos de operación de DPMO por procesos
Cada uno de los procesos del sistema productivo presentó una evolución positiva, con una tendencia decreciente de los defectos a medida que se incrementó el nivel Sigma.
Proceso 1: en este proceso, con un nivel Sigma inicial de 3.88, se identificaron 2.405 no conformidades, con un DPMO de 8.294 y un rendimiento del 99,17%, a pesar de ello, conforme se implementaron mejoras y el nivel Sigma se incrementó a 6.43, se logró eliminar por completo los defectos, alcanzando un rendimiento del 100%, ya que, este proceso destaca por haber alcanzado una optimización completa en su desempeño.
Proceso 2: en este caso, el nivel Sigma inicial fue de 3.30, lo que resultó en 4.811 no conformidades y un DPMO de 34.894,65, a medida que se avanzó hacia un Sigma de 5.75, los defectos se redujeron a solo uno, y el rendimiento aumentó al 100%, puesto que, este proceso mostró una mejora sostenida, evidenciando la efectividad de las medidas implementadas.
Proceso 3: con un Sigma inicial de 3.25, el proceso 3 presentó 4.811 no conformidades y un DPMO de 39.476,08, aunque, al incrementar el Sigma a 6.11, se logró eliminar todos los defectos, alcanzando también un rendimiento del 100%, debido a que, la evolución de este proceso sigue un patrón similar al del proceso 2, mostrando una clara mejora conforme se aumentó el nivel Sigma.
![]()
Proceso 4: este proceso comenzó con un nivel Sigma de 3.50, un DPMO de 21.958,74 y un rendimiento del 97,80%, a medida que el nivel Sigma alcanzó 6.24, se logró eliminar todos los defectos, lo que resultó en un rendimiento del 100%, de modo que, este proceso demostró una mejora gradual en su desempeño, lo que sugiere que las medidas de mejora continua fueron implementadas de manera eficiente y consistente.
Proceso 5: al inicio del análisis, con un Sigma de 3.57, se identificaron 3.207 no conformidades y un DPMO de 18.532,73, con un rendimiento del 98,15%, a pesar de ello, conforme se incrementó el Sigma a 6.27, los defectos se eliminaron por completo, y el proceso alcanzó un rendimiento del 100%, ya que, este proceso destaca por su rápida mejora en comparación con otros procesos del sistema.
Proceso 6: en este caso, el nivel Sigma inicial fue de 3.77, con 3.207 no conformidades y un DPMO de 11.364,39, conforme el Sigma se incrementó a 6.37, los defectos fueron completamente eliminados, alcanzando un rendimiento del 100%, debido a esto, el proceso mostró una evolución favorable, especialmente a partir de un nivel Sigma de 4.5, donde las mejoras en la calidad se hicieron más evidentes.
Proceso 7: este proceso, que comenzó con un Sigma de 3.52 y 9.621 no conformidades, mostró una mejora notable al incrementar el Sigma a 6.25, donde se eliminaron los defectos y se alcanzó un rendimiento del 100%, puesto que, el proceso 7 fue uno de los que más defectos presentó al inicio, pero las intervenciones implementadas permitieron una mejora considerable en su desempeño.
Impacto global de la metodología Seis Sigma
El análisis de los resultados confirma que la metodología Seis Sigma fue efectiva para mejorar el desempeño del sistema productivo integrado. Las curvas de operación de DPMO y de porcentaje de rendimiento (Y) muestran una relación clara entre el aumento del nivel Sigma y la reducción de defectos en todos los procesos evaluados. Además, el rendimiento de cada proceso mejoró significativamente, alcanzando valores cercanos al 100% en la mayoría de los casos.
A nivel global, el sistema productivo experimentó una mejora continua a medida que se implementaron las estrategias de mejora propuestas. A partir de un nivel Sigma de 4.5, se observaron mejoras significativas en todos los procesos, lo que sugiere que este umbral es crucial para garantizar una producción libre de defectos. Los procesos más complejos, como el proceso 7, también mostraron
![]()
mejoras notables, lo que indica que las estrategias Seis Sigma son eficaces incluso en escenarios más desafiantes.
Hallazgos
La implementación de las métricas Seis Sigma y las curvas de operación en el sistema productivo integrado reveló una serie de hallazgos relevantes para el mejoramiento del desempeño del proceso. En primer lugar, se observó una reducción característica en la cantidad de productos defectuosos por millón de oportunidades (DPMO) en los diferentes procesos evaluados. Por otro lado, los resultados indicaron una disminución gradual en los niveles de defectos, especialmente a medida que se optimizaban los niveles sigma. En particular, procesos clave dentro del sistema, como los procesos 1, 5 y 7, mostraron mejoras sustanciales, alcanzando niveles sigma superiores a 5.0, lo que indica una casi eliminación de defectos, con un DPMO inferior a 200.
Desde otra perspectiva, el rendimiento (Y) también mostró una tendencia ascendente en todos los procesos, con valores que oscilaron entre el 99.17% y el 100%, evidenciando una optimización general del sistema. El proceso global, que inició con un nivel sigma de 3,0 y un rendimiento del 93.43%, logró alcanzar un nivel sigma de 6.0, lo que representó una casi total eliminación de productos defectuosos, con un rendimiento del 100%. Por ello, esto confirma que la implementación de las métricas Seis Sigma impactó positivamente en la eficiencia global del sistema productivo, logrando una mayor consistencia en la calidad de los productos.
Ahora bien, otro hallazgo transcendental fue la efectividad de las curvas de operación para predecir y ajustar la variación en los diferentes procesos, puesto que, estas curvas permitieron visualizar las relaciones entre los niveles sigma y los DPMO, lo que facilitó la identificación de puntos críticos dentro del proceso productivo y permitió aplicar ajustes precisos en las etapas necesarias para reducir la variabilidad. Debido a ello, este enfoque fue particularmente útil para ajustar los procesos con un rendimiento inicial más bajo, como el proceso 2, que mejoró su nivel sigma de 3,30 a 5,75 a lo largo de la investigación.
Los resultados obtenidos en este estudio presentan tanto similitudes como diferencias con estudios previos que han utilizado la metodología Seis Sigma. En consonancia con investigaciones como la de Estrellas (2022), la implementación de las métricas Seis Sigma generó una mejora
![]()
sustancial en el control de calidad del sistema productivo, reduciendo defectos y optimizando el rendimiento general.
A pesar de ello, a diferencia de estudios previos que se centraron en la mejora de procesos en sectores más tradicionales como la manufactura de muebles o automóviles, nuestro estudio aplicó la metodología Seis Sigma en un sistema productivo integrado de alta complejidad. Del mismo modo, este tipo de sistema, al involucrar múltiples procesos interrelacionados, presentó desafíos adicionales que fueron solventados mediante la construcción de curvas de operación más precisas y la aplicación constante de métricas Seis Sigma.
A diferencia de investigaciones anteriores, en este estudio se observó una mayor efectividad en la reducción de defectos en un menor número de iteraciones, lo que puede atribuirse al enfoque sistemático y proactivo en la construcción de las curvas de operación y su uso constante como herramienta de monitoreo. Mientras que Tologasí (2018), reportaba que se necesitaban múltiples ciclos de mejora para alcanzar un nivel sigma de 4.0, en nuestro estudio se lograron niveles sigma de hasta 5.0 en un menor número de ciclos de ajuste, lo que representa una ventaja competitiva en términos de tiempo y recursos.
Conviene subrayar que, otro punto diferenciador es el uso de curvas de operación más detalladas, que permitieron una intervención más rápida en puntos críticos del proceso. De acuerdo con estudios como el de Irigoin et al., (2023), no detallaban con tanta profundidad el uso de este tipo de herramientas gráficas para el monitoreo continuo, lo que posiciona nuestro estudio como una referencia clave en la aplicación de Seis Sigma en sistemas de producción integrados.
Debido a lo establecido en este estudio, en cuanto a los valores Sigma, este estudio identificó un nivel óptimo entre 5.1 y 6.0 para la mayoría de los procesos, lo que difiere de estudios previos que se conformaron con niveles Sigma alrededor de 4.5. Este incremento se debe, en parte, a la integración de las curvas de operación, que proporcionaron una visión más detallada y permitieron ajustar de manera más precisa los controles de calidad.
Por otro lado, es importante mencionar que los estudios anteriores no desarrollaron estrategias de mejora específicas basadas en los valores Sigma obtenidos para cada proceso. En este estudio, se propusieron estrategias de mejora que incluyeron la optimización del flujo de trabajo, la reducción de variabilidad en los procesos críticos y la implementación de controles adicionales para asegurar que los niveles Sigma se mantengan altos a lo largo del tiempo.
![]()
Este estudio demostró que la implementación de métricas Seis Sigma, combinadas con el desarrollo de curvas de operación, resultó en una mejora sustancial del desempeño de un sistema productivo integrado. A través de la evaluación de los procesos, se logró determinar los niveles Sigma específicos de cada uno, identificando oportunidades de mejora clave para reducir la cantidad de productos defectuosos.
El objetivo general de mejorar el desempeño del sistema mediante la optimización del nivel Sigma se alcanzó con éxito. En términos de los objetivos específicos, se evaluó de manera exhaustiva el sistema productivo utilizando indicadores Seis Sigma, lo que permitió determinar los niveles de calidad de cada proceso. Por otra parte, se desarrollaron curvas de operación que facilitaron la visualización del desempeño del sistema global y de los procesos individuales, proporcionando información crucial para la toma de decisiones en la optimización de los mismos.
Desde otra perspectiva, se propusieron estrategias de mejora enfocadas en alcanzar y mantener niveles Sigma altos, con el objetivo de reducir de manera permanente los defectos junto con el hecho de mejorar la eficiencia operativa. Los hallazgos obtenidos reafirman la importancia de una metodología estructurada como Seis Sigma para incrementar la competitividad y la calidad en sistemas productivos integrados.
Ana Milena Calabria Ramos. Facultad de Ciencias Económicas, Universidad de Cartagena.
Cartagena, Colombia. Correo electrónico: acalabriar@unicartagena.edu.co
Tomas Fontalvo Herrera. Facultad de Ciencias Económicas, Universidad de Cartagena.
Cartagena, Colombia. Correo electrónico: tfontalvoh@unicartagena.edu.co.
Los autores han participado en la redacción del trabajo y análisis de los documentos
![]()
Aizaga, M. R. (2022). Diseño e implementación de Six Sigma para la mejora del proceso de secado la empresa secado y tratado de madera Cia. Ltda. Bachelor's thesis. https://dspace.ups.edu.ec/handle/123456789/22731
Bonilla, G. C. (2020). Análisis de los factores determinantes del Lean Six Sigma en la productividad y competitividad de las Pymes colombianas. Universidad EAN. http://hdl.handle.net/10882/10291
Estrella, C. K. (2022). Implementación del sistema de gestión integral de seguridad salud en el trabajo, medio ambiente y calidad para lograr una mejora continua en la Empresa SIERRA POLI SAC. Universidad Nacional del Centro de Perú. http://hdl.handle.net/20.500.12894/9066
Fernández, A. C., et al. (2020). El Estado en la era exponencial. Instituto Nacional de la Administración Pública. https://doi.org/10.29265/gypp.v30i1.846
Fleaca, B. C. (2019). Critical to Quality (CTQ) tree technique to improve teaching and learnig process the case of higher eduction. Univerity Politehnica. ISBN 978-80-88085-24-9 https://books.google.es/books?hl=es&lr=&id=dIanDwAAQBAJ&oi=fnd&pg=PA130&dq= CTQs+(Critical+to+Quality)+pdf&ots=Xy65mSpnQm&sig=V5Egc- eKB2U0SaohL23QsgytdB8#v=onepage&q&f=false
Fontalvo, H. T. (2024). Evaluación con curvas de operación de métricas Seis Sigma el desempeño de sistemas productivos mixtos. Investigación e Innovación en Ingenierías. https://doi.org/10.17081/invinno.11.2.6680
Franco, A. I. (2021). Aplicación de Metodología DMAIC para la reducción de defectos en la liberación de producto terminado. Universidad Autónoma de Baja California. https://hdl.handle.net/20.500.12930/359
García González, R.., Juárez León, S., Guevara Ramírez, I., & García Pérez, J. E. C. (2021). DMAIC – SIX SIGMA. Revista RELAYN. Micro y Pequeña empresa en Latinoamérica, 5(3), 164-190. http:// doi.org/329/3292837009/
![]()
Garza et al., R. R. (2016). Aplicación de la metodología DMAIC de Seis Sigma con simulación discreta y técnicas multicriterio. Revista de Métodos Cuantitativos para la Economía y la Empresa. http://www.redalyc.org/articulo.oa?id=233148815002
Guerrero M. D. et al., (2019). Revisión de la implementación de Lean Six Sigma en Instituciones de Educación Superior. Ingeniare. Revista chilena de ingeniería.
/http://dx.doi.org/10.4067/S0718-33052019000400652
Irigoin, C. U. et al., (2023). Métodos estadísticos para el control de la calidad y la productividad. Editorial Mar Caribe de Josefrank Pernalete Lugo. https://doi.org/https://hcommons.org/deposits/item/hc:62105
Jurado, A. E. (2019). Propuesta para implementar Lean Seis Sigmas en el departamento de servicio al cliente en una empresa del sector Retail. Universidad de la Salle. https://ciencia.lasalle.edu.co/ing_industrial/108
Marin C. A. et al., (2022). Aplicación de la metodología Lean Six Sigma para disminuir desperdicios en una unidad de fabricación de páneles modulares de poliestireno. Universidad Nacional Autónoma de México. https://doi.org/10.22201/fi.25940732e.2023.24.1.007
Ortiz, T. M. (2020). Implementación del modelo Six Sigma estrategia de mejora en Pymes de Latinoamérica. Fundación Universidad de América. https://hdl.handle.net/20.500.11839/7868
Salazar, L. B. (2019). Nivel Sigma y DPMO. Revista de ingeniería industrial. https://www.academia.edu/40941696/Control_estadistico_de_la_calidad_y_Seis_Sigma_H umberto_Gutierrez_Pulido20191115_15423_1h57201
Simón, M. K. (2024). Plan estratégico de mejora de procesos de permisos de construcción en el Distrito Central, Honduras 2024. Universidad Tecnológica Centroamericana UNITEC. https://repositorio.unitec.edu/items/650cf697-b601-4a46-95c1-76ae457cecb9/full
Tolagasí, S. G. (2018). Mejoramiento de la capacidad del proceso de impresión de la compañia Sigmaplast a través de la aplicación de la metodología Seis Sigma. Escuela Politécnica Nacional. http://bibdigital.epn.edu.ec/handle/15000/19084
![]()
Victorio, P. Ó. (2020). Implantación de un sistema de Lean Manufacturing y mejora continua en una industria jabonera. Universidad Politecnica de Cartagena. http://hdl.handle.net/10317/8884